巴恰塔亚模型发表评论(0) 编辑词条

巴恰塔亚模型概述编辑本段 回目录

　　1979年，巴恰塔亚将其1977年在麻省理工学院所作的博士论文中的一章整理后发表在《贝尔经济学刊》上。在文中，他构建了一个与罗斯模型非常相近的股利信号模型。巴恰塔亚认为，在不完美情况下，现金股利具有的信息内容，是未来预期盈利的事前信号。

巴恰塔亚模型的内容编辑本段 回目录

　　巴恰塔亚模型假设：

　　(1)企业拥有的资产可以产生无限期的现金流；

　　(2)现有资产产生的所有现金流量都可以理性地再投资；

　　(3)股利决策是由内部管理者做出的，由于其奖金与股东财富相联系，所以内部管理者的经营目标是股东财富最大化；

　　(4)只有内部管理者惟一知道现金流量分布信息；

　　(5)风险中性；

　　(6)期限为一年。

　　用X表示从新项目所获得的不确定性的现金流量，现金股利的个人所得税率为 $1 - α$ ，资本利得不征税，D表示新增发的股利，V(D)表示因新增股利而增加的清算价值。

　　如果 $X > D$ ，则现有股东将获得税后股利 $α D$ ，企业再投资需要从外部筹集的资金减少 $(X - D)$ 元。

　　如果 $X < D$ 如，企业支付的股利仍为D，资金不足部分(D—x)将给现有股东带来 $(1 + β)(D - X)$ 的成本。所以，现有股东的新增价值函数为:

　　 $E(D)=\frac{1}{1+r}\left[ V(D)+\alpha D+\int_D^{\overline{X}}(X-D)f(X)dX+\int_{\underline {X}}^D(1+\beta)(X-D)f(X)dX \right]$

　　 $=frac{1}{1+r}\left[ V(D)+M-(1-\alpha)D-\beta \int_{\underline {X}}^D F(X)dX \right]$ ……(1)

　　式中： $f (X)$ 和 $F (X)$ 为X在区问 $(\underline {X},\overline{X})$ 的密度函数和分布函数；M为现金流量的平均值；r为贴现率。

　　假设投资项目的现金流量分布在 $[0, t]$ ，平均值为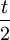 $\frac{t}{2}$ ，各个企业的t大小不同，最小值为 $t m i n$ ，最大值为 $t m a x$ ，但是投资者无法区分t的大小。为此，作为企业股东的代理人，管理者通过股利支付决策向外发射信号帮助投资者区分t，并使自己的报酬最大化，即:

　　 $max E(D)=max \left\{ \frac{1}{1+r}\left[ \frac{t}{2}+V(D)-(1-\alpha)D-\beta \frac{D^2}{2t} \right] \right \}$ ……(2)

　　求导，得:

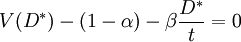　　 $V(D^*)-(1-\alpha)-\beta\frac{D^*}{t}=0$ ……（3）

　　巴恰塔亚认为，只有当预期现金流量实现了，即V(D)与股利信号显示的价值一致时，才能达到均衡。相对于资本利得来讲，股利传递信息的价值是确定的，而且它可以用来抵消股利所得的税收损失，从而即使管理层控制权力很大的公司也乐于支付股利，因为只有当股利分配方案向外界披露后，该信息引起的公司价值增值才能够为现有的股东所获得。

巴恰塔亚模型发表评论(0) 编辑词条

巴恰塔亚模型概述编辑本段 回目录

巴恰塔亚模型的内容编辑本段 回目录

相关条目编辑本段 回目录

附件列表

巴恰塔亚模型 发表评论(0) 编辑词条

巴恰塔亚模型概述编辑本段回目录

巴恰塔亚模型的内容编辑本段回目录

相关条目编辑本段回目录

附件列表

巴恰塔亚模型发表评论(0) 编辑词条