投入产出表 发表评论(0) 编辑词条
什么是投入产出表[1]编辑本段回目录
投入产出表的产生编辑本段回目录
投入产出表在二十世纪三十年代产生于美国,它是由美国经济学家、哈佛大学教授瓦西里·列昂惕夫(W.Leontief)在前人关于经济活动相互依存性的研究基础上首先提出并研究和编制的。
列昂惕夫从1931年开始研究投入产出技术,编制投入产出表,目的是研究美国的经济结构。1936年他撰写的“美国经济制度中投入产出数量关系”在《经济学和统计学评论》上发表。它是世界上有关投入产出技术的第一篇论文,标志着投入产出技术的诞生。1953年列昂惕夫与他人合作,出版了《美国经济结构研究》一书。通过这些论著,列昂惕夫提出了投入产出表的概念及其编制方法,阐述了投入产出技术的基本原理,创立了投入产出技术这一科学理论。正是在投入产出技术方面的卓越贡献,列昂惕夫于1973年获得了第五届诺贝尔经济学奖。
投入产出表的发展编辑本段回目录
投入产出技术从诞生到现在的七十多年里,无论是在理论方面,还是在实践方面都得到了很大的发展,取得了丰硕成果。早期的投入产出模型,只是静态的投入产出模型。后来,随着研究的深入,开发了动态投入产出模型,投入产出技术由静态扩展到动态。近期,随着投入产出技术与数量经济方法等经济分析方法日益融合,投入产出分析应用领域不断扩大。
五十年代末六十年代初,我国经济理论界和一些高等院校的少数同志开始研究投入产出技术,某些高等院校还开设了投入产出技术课程。“文革”期间,此项工作几乎中断。1974年8月,为研究宏观经济发展情况的需要,在国家统计局和国家计委的组织下,由国家统计局、国家计委、中国科学院、中国人民大学、原北京经济学院等单位联合编制了1973年全国61种产品的实物型投入产出表。利用该表开展的应用工作,在制定投资计划和产品生产计划等方面发挥了积极的作用。
十一届三中全会以后,党和国家把工作重点放到经济建设上,这就为包括投入产出技术在内的现代经济分析方法的研究和应用创造条件。从此开始投入产出表的编制工作,投入产出技术的研究和投入产出表的应用工作得到了迅速的发展。
1980年,按照国家统计局的要求,山西省统计局编制了山西省1979年投入产出表,为编制全国投入产出表提供了经验。
1982年,国家统计局、国家计委及有关部门编制了1981年全国投入产出价值表和实物表。
1984年,在1981年全国投入产出价值表的基础上,国家统计局编制了1983年全国投入产出延长表。
1987年,除个别地区外,各省(自治区、直辖市)都编制了本地区投入产出表;一些管理部门还编制厂部门投入产出表;一些企业也编制了企业投入产出表。
1987年3月底,为了适应改革开放的需要,为加强国民经济宏观调控和管理,提高经济决策的科学性,国务院办公厅发出了《关于进行全国投入产出调查的通知》(国办发[1987]18号),明确规定每五年(逢二、逢七年份)进行一次全国投入产出调查和编表工作。1987年,我国进行了第一次全国性的投入产出调查和编表工作。《1987年全国投入产出表》的编制成功和在宏观经济调控等方面的成功应用,标志着投入产出技术在我国发展到一个新的阶段。
1992年,国家统计局在1987年全国投入产出表的基础上,编制了1990年投入产出延长表。
1994年和1995年,国家统计局先后编制了1992年全国出价值表和实物表。1992年全国投入产出表为国民经济核算体系全面转轨提供了数据依据。
1996年,国家统计局在1992年全国投入产出表的基础上,编制了1995年全国投入产出延长表。
1999年,国家统计局编制了1997年全国投入产出表。
到目前为止,除西藏以外,全国三十个省(自治区、直辖市)与国家同步编制了1987、1992和1997年本地区投入产出表。部分省(自治区、直辖市)还编制了1990年、1995年和2000年本地区投入产出延长表。今年开始进行第五次全国投入产出调查,并编制2007年全国投入产出表。
投入产出技术不仅在我国宏观和微观经济领域获得了广泛的应用,而且在微观经济领域的应用也取得了可喜的成绩。目前,已有一些企业编制了企业投入产出表,并用于企业计划、生产、成本等管理工作中。
投入产出表的分类[1]编辑本段回目录
- 按计量单位分:价值型和实物型;
- 按表式结构分:对称型(纯部门)和U-V型(UV表法);
- 按资料范围分:全国表、地区表和企业表;
- 按时间期限分,静态表和动态表;
- 按考察领域分:产品表,固定资产表、能源表、人口表、教育表、环境污染表,等等。
投入产出表的四大象限[1]编辑本段回目录
暂不考虑作为合计数的“总投入”行与“总产出”列以及生产部门的“小计”栏,可将投入产出表划分为四大象限,分别表达特定的经济内容。
(1)第Ⅰ象限(中间产品或中间消耗):核心。反映各部门之间相互提供、相互消耗产品的技术经济联系。
第Ⅰ象限的特点:
- 横行标题和纵栏标题是名称、排序相同的产品部门,具有严整的棋盘式结构;
- 横行~提供中间产品的部门(产出部门);纵栏~消耗中间产品的部门(投入部门);表中每项数据都具有“产出”与“消耗”的双重涵义。
- 该象限的所有n2 个数据组成“中间流量(中间产品、中间消耗)矩阵”:
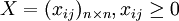
(2)第Ⅱ象限(最终产品或最终使用):反映各部门提供最终产品的数量和构成情况(可以细分为消费、投资和净出口)。
其数据组成“最终产品列向量”:
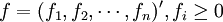
(3)第Ⅲ象限(最初投入或增加值):反映各部门的最初投入数量及其构成(可以细分)。其数据组成“最初投入(增加值)行向量”:
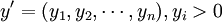
(4)第Ⅳ象限:空白(可在国民核算矩阵中适当开发)。
投入产出表的两个方向[1]编辑本段回目录
横表:Ⅰ+Ⅱ,反映各部门的产出及其使用去向,即“产品分配”过程;
竖表:Ⅰ+Ⅲ,反映各部门的投入及其提供来源,即“价值形成”过程。
“横表”和“竖表”各自存在一定的平衡关系,彼此之间又在总量上相互制约,构成投入产出表建模分析的基础框架。
投入产出表的平衡关系[1]编辑本段回目录
投入产出表的基本平衡关系有如下三种:
(一)各行(横表)的平衡──产品平衡方程:
中间产品+最终产品=总产出

(二)各列(竖表)的平衡──价值平衡方程:
中间投入+最初投入=总投入
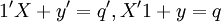
(三)各行列(横表和竖表)的对应平衡:
各部门总产出=该部门总投入
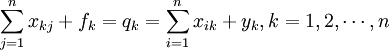
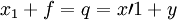
这表明:“产品平衡方程”与“价值平衡方程”既相对独立,又相互制约。
从投入产出表所有行列的角度看,有:
- 所有部门的总产出=所有部门的总投入,即:
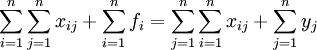
- 所有部门的中间产品=所有部门的中间消耗,即:
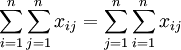
从而有:
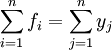
即:所有部门提供的最终产品=所有部门创造的增加值。
但应注意:
- 每个部门所提供的中间产品价值与其消耗的中间产品价值通常不等,即:
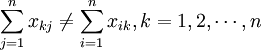
- 每个部门所提供的最终产品价值与其创造的增加值通常也不等,即:
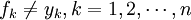
投入产出表的作用编辑本段回目录
投入产出表可全面系统地反映国民经济各部门之间的投入产出关系,揭示生产过程中各部门之间相互依存和相互制约的经济技术联系。一方面它能告诉人们国民经济各部门的产出情况,以及这些部门的产出是怎样分配给其它部门用于生产或怎样分配给居民和社会用于最终消费或出口到国外的;另一方面它还能告诉人们,各部门为了自身的生产又是怎样从其它部门取得中间投入产品及其最初投入的状况。投入产出核算的功能不仅仅在于反映现各个部门在生产过程中直接的、较为明显的经济技术联系,更重要的是它揭示出各部门之间间接的、较为隐蔽的、甚至被人忽视的经济技术联系。投入产出表为研究产业结构,尤其为制定和检查国民经济计划,研究价格决策,进行各种定量分析提供依据。
投入产出表的缺陷编辑本段回目录
投入产出表的起源不明,有人误认为起源于魁奈的经济表和马克思的再生产公式——这是不可能的。它们的核心是货币回流规律,当转换成投入产出表后,再也看不到货币回流了;投入产出表的实物形态与价值形态分离;用列昂惕夫逆阵计算完全消耗系数,只有结果,没有过程;不能反映流通过程,不适应市场经济的需要;不能反映再分配过程,等等。这些缺陷都通过再生产平衡表得以克服。再生产平衡表具有更多的优越性。
参考文献编辑本段回目录
↑ 1.0 1.1 1.2 1.3 1.4 杨灿.《国民经济统计学》[M]第4章 投入产出核算
相关词条编辑本段回目录
本词条由以下会员参与贡献
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
3

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
