表上作业法 发表评论(0) 编辑词条

　　表上作业法是指用列表的方法求解线性规划问题中运输模型的计算方法。是线性规划一种求解方法。当某些线性规划问题采用图上作业法难以进行直观求解时，就可以将各元素列成相关表，作为初始方案，然后采用检验数来验证这个方案，否则就要采用闭合回路法、位势法等方法进行调整，直至得到满意的结果。这种列表求解方法就是表上作业法。

　　1、找出初始基本可行解（初始调运方案，一般m+n-1个数字格），用西北角法、最小元素法；

　　（1）西北角法：

　　从西北角（左上角）格开始，在格内的右下角标上允许取得的最大数。然后按行（列）标下一格的数。若某行（列）的产量（销量）已满足，则把该行（列）的其他格划去。如此进行下去，直至得到一个基本可行解。

　　（2）最小元素法：

　　从运价最小的格开始，在格内的右下角标上允许取得的最大数。然后按运价从小到大顺序填数。若某行（列）的产量（销量）已满足，则把该行（列）的其他格划去。如此进行下去，直至得到一个基本可行解。

　　注:应用西北角法和最小元素法，每次填完数，都只划去一行或一列，只有最后一个元例外（同时划去一行和一列）。当填上一个数后行、列同时饱和时，也应任意划去一行（列），在保留的列（行）中没被划去的格内标一个0。

　　2、求出各非基变量的检验数，判别是否达到最优解。如果是停止计算，否则转入下一步，用位势法计算；

　　运输问题的约束条件共有m+n个，其中：m是产地产量的限制；n是销地销量的限制。其对偶问题也应有m+n个变量，据此：

　　σ_ij = c_ij − (u_i + v_j) ,其中前m个计为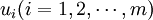,前n个计为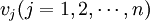

　　由单纯形法可知，基变量的σ_ij = 0

　　c_ij − (u_i + v_j) = 0因此u_i,v_j可以求出。

　　3、改进当前的基本可行解（确定换入、换出变量），用闭合回路法调整；

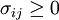　　（因为目标函数要求最小化）

　　表格中有调运量的地方为基变量，空格处为非基变量。基变量的检验数σ_ij = 0，非基变量的检验数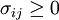。σ_ij < 0表示运费减少,σ_ij > 0表示运费增加。

　　4、重复②，③，直到找到最优解为止。

　　1、无穷多最优解

　　产销平衡的运输问题必定存最优解。如果非基变量的σ_ij = 0，则该问题有无穷多最优解。

　　2、退化

　　表格中一般要有(m+n-1)个数字格。但有时，在分配运量时则需要同时划去一行和一列，这时需要补一个0，以保证有(m+n-1)个数字格。一般可在划去的行和列的任意空格处加一个0即可。

• 图上作业法