进化对策论 发表评论(0) 编辑词条
进化对策论概述 编辑本段回目录
最近10多年里,不像对策论的传统分析方法那样——考虑有限理性的经济行为人以及在严格的认知局限之下必须学习执行策略,这样的对策论理论及其应用有了迅速的发展。这方面的大量研究工作是在称为进化对策论所提供的框架下进行的。正如此学科标题所表示的,这一新学科的原理借用生物学中的进化模型所具有的与众不同的一些特征。然而,此学科本身也发展了一些新的方法和技术,特别地适合于有限理性基本假设下对社会和经济体制方面的分析。进化对策论在10多年里以快速的步伐取得长足的发展。
进化对策沦为人们提供一种具有广泛适用性的工具。其潜在的应用领域从进化生物学延伸到一般的社会科学,特别是经济学中。进化理论在经济学中有着悠久的历史传统。直到最近,这种方法在非合作对策论框架中才得到应用。
进化对策论是研究策略行为的稳健性,它是针对有限理性行为人所组成的大群体中多次博弈背景下的进化力量而言的。这种新的组成部分在经济理论里导致一种新的预测方法,并且为其他社会科学开辟一条崭新的研究途径。
进化对策论的基本内容 编辑本段回目录
(一)进化稳定策略概念
进化对策论理论中,一个关键概念是进化稳定策略(ESS),这一概念的提出归功于约翰·梅纳德·史密斯(John Maynard Smith)和普莱斯在1973年的“动物冲突的逻辑”一文。此种策略在特定的意义上对进化压力而言是稳健的:群体执行该种策略对执行任何其他策略而言是非入侵的。假定一对个体是重复随机地来自于大的群体,去参与一个对称并有限的两人博弈,还假定所有的个体在博弈中起初都执行某一个纯的或混合的策略x是进化稳定的,那么对于每一个变异策略y,都存在一个正的“入侵障碍”,使得执行变异策略y的个体群体所获得的支付低于此障碍,从而x赢得的预期支付比执行的y所得要高。下面的不等式对于充分小的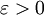 成立,即:
成立,即:
u[x,(1-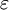 )x+
)x+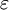 y]>u[y,(1-
y]>u[y,(1-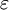 )x+
)x+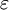 y]…………(1)
y]…………(1)
其中左边的表达式记为对于策略x而言,当执行相对应策略的个体进入之后,混合群体情况的混合策略(1-ε)x+εy时的预期支付,而右边的表达式记为对于策略y而言,其所对应的情况的预期支付。
注意到,进化稳定性准则没有解释种群是如何达到这种策略的。然而,一旦达到这种策略,则这样的策略对进化压力来说是稳健的。同时,人们发现,进化稳定性没有处理种群中具有两个或更多“变异”同时出现的情况。因而,它隐含地把变异当成稀少事件,以致于种群有时间在另一个变异出现之前响应这种状况。
虽然,进化稳定性准则是一个生物学上的概念,但是它为各种各样的人类行为提供一种有关的稳健性准则。这样,进化稳定性要求人类群体中企图采用可选择的策略的任何一个小团体不比已经采用“固有”策略的那些个体所构成的团体收益好。相反,采用固有策略的那些个体所构成的团体缺乏激励来改变他们的策略。但是,那些采用可选策略的小团体却受激励而具有转变固有策略的行为。在这种社会背景下,进化稳定策略被人们看成是传统习惯或者已经确立起来的行为规则。比如,社会风气、企业管理模式等都可以看为是某种人类群体的规则,而极个别的人群社会行为、习气的变化就会被认为是“变异”。当然,在这种背景下,如果那些极少数的人群或企业的收益比不变异的人群或企业高时,那么这些变异分子会生存得更好!反之,则被淘汰掉。
可惜的是,许多博弈没有进化稳定策略。于是,研究人员探讨各种比进化稳定性稍弱一些的形式,以及集值形式的进化稳定性概念等。此外,ESS概念不能推广到n人对策的情况上。在本质上,ESS要求强的纳什均衡来实施,也就是每一个策略对于策略组而言应是唯一的最佳反应。
(二)复制动力学
复制动力学是选择过程的显性模型,它说明种群是如何分配博弈中有联系的不同纯策略随时间而演化的。复制动力学的数学公式是由 Taylor和Jonker于1978年在“进化稳定策略和对策动力学”一文中提出的。他们认为由随机配对的个体所构成的一个大种群执行有限对策的两人博弈,犹如进化稳定性的设置一样。然而,此处的个体仅仅采用纯策略。种群状态是指在纯策略上的一个分布x。这种状态在数学上与博弈中的混合策略是等价的。
如果博弈中的收益表示成生物学上的适合性,也就是后代的数目,同时每一个后代继续其父母的策略,因此,采用纯策略i的个体数目(在大的种群中)将以某一比率指数增长,而此等于对纯策略i的预期收益u(ei,x),当执行着表示种群中当前策略分布的混合策略x时,采用任何纯策略i的种群分布的增长率等于此策略的收益与种群中平均收益的差。后者,等同于混合策略x当与其自身博弈时的预期收益u(x,x)。这是一个单种群的对称两人博弈的复制动力学。
Xi=[u(ei,x)-u(x,x)]xi………………(2)
注意到,对当前种群状态x的最佳反应具有最高的增长率。第二最佳反应具有第二高的增长率,如此等等。然而,虽然更成功的纯策略比欠成功的纯策略增长得快,但是种群中的平均收益不必随时间而增长。产生这一原因的可能性是,如果一个个体由采用最佳策略的个体所代替,那么遇见这个新个体的成员会得到比较低的收益。例如,这正是囚徒困境博弈的情况。如果最初几乎所有个体采用“合作”,那么个体中将逐渐地转向“抵赖”,从而平均收益将下降。然而,如果博弈在两个人总是获得相等的收益意义上是一个双对称的,那么自然选择的基本规律将成立:种群中收益随时间而增长,即使没有必要成为全局最大的。例如,这就是合作博弈的情况,其中所有个体逐渐地转向到执行同一个纯策略上。复制动力学能够推广到n人博弈的情况上,这可以看成是来自于 n种群、中的个体随机地以n类型配对,其中每一个参与者的地位状况正如纳什所给出的群体行为解释的那样。目前,存在两种形式的n种群复制动力学,其中一个是由Taylor在 1979年提出的,另一个是由Maynard Smith在1982年给出的。
(三)学习模型
人们把学习模型分成三种类型,即基于信念的学习、强化学习以及模仿学习。最近的一些研究表明,复制动力学是由后面两类的某种模型所促成的。
1.强化学习模型
Bush和Mosteller的强化学习模型及其他的推广形式,已经在一系列的人类主观执行博弈中得到运用。可惜,这些模型的通常数学性质,人们还知道得很少。然而,Borgers和Sarin在1997年发表的“通过强化和复制动力学的学习”文章把Cross的Bush—Mosteller学习模型的形式与Taylor的两种群复制动力学进行了理论上的对比研究。虽然这种学习过程在离散时间背景中是随机的、演化的,而复制动力学在连续时间背景中是确定的、演化的。他们证明,在适当地构造连续时间的界限下,他们的学习过程在有限时间区间内可通过复制动力学来说明。
2.模仿学习模型
博弈论学者Gale,Binmore和Samuelon在1995年提出一个所有个体参与者都采用纯策略的大群体,但是有限博弈的社会学习的简单模型。每一个参与者在博弈中都赢得一个渴望水平的收益。在离散时间0,δ,2δ,…上,任意从群体中抽取个体δ部分,把其当前收益与他们的渴望水平收益相比较,其中δ>0是很小的数。如果个体实现的收益低于其生存水平收益,那么该个体就会随机地模仿已抽取的个体,在相同的参与者群体中,所有其他个体都具有相同的概率被抽取。由此可见,如果渴望水平收益具有均匀分布(某一个区间上包含所有可能的收益值),那么模仿的概率对于个体的当前策略而言,在预期收益上是线性递减的。对于很小的δ,他们证明这个过程可以由有限时间区间上的复制动力学来说明。
进化对策论在经济学中的应用 编辑本段回目录
进化对策论的产生、发展在本质上就是起因于对策论中关于理性行为人的假设与经济应用中行为人“试验——失误”(即试错法)学习过程相偏离的事实而引发的。从上述的阐述中,我们可以看到,进化对策论在经济学里的应用前景是十分广阔的和吸引人的。
最近,Routledge探讨了金融市场上个体行为人是如何通过适应性或者进化学习来发现内生变化并运用这种内生关系的一种学习模型。他通过对来自于模仿过程和经验过程来对个体的投资行为建模,而不是运用传统上的显性最优化方法放松关于知识和理性的假设。Routledge运用Grossman和Stiglitz的1980年发表的经济模型的形式。Grossman和Stiglitz模型(GS模型)提供了考察适应学习过程的一种良好的框架,因为它是获得内生信息的标准模型,这点已经被后来的其他许多关于学习方面的模型都是基于GS而提出的事实所证明。
如果假设交易者能够观察到他们自己的适应度和其他行为人的行为,那么模仿是如何发生的许多特殊细节就显得不重要了。Routledge的研究结果表明:首先,作为单调选择动力学的适应学习会促成GS均衡;其次,由单凋适应学习驱使的模仿的稳健性可从随机实验中来获得噪声来研究。他发现,适应学习是缺少稳健性的。特别,他运用Binmore和Samuelson的技术来对模仿和经验建模。为了使带有漂移的适应学习产生GS理性预期均衡,必要的条件是在风险资产供给中的噪声与学习过程中的经验水平有很大的关系。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 进化对策论 ESS Grossman John Maynard Smith 企业管理模式 供给 博弈论 合作博弈 囚徒困境 对策论 平均收益

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
