跨期资本资产定价模型 发表评论(0) 编辑词条

跨期资本资产定价模型（Intertemporal Capital Asset Pricing Model 或 Intertemporal CAPM，简称ICAPM），也称瞬时资本资产定价模型

　　在资产定价理论中的另一个重要假设是：证券市场总是在连续过程中，在这一假设前提下，Merton(1969,1971)将CAPM发展为跨期资本资产定价模型(ICAPM)，同样在信息对称、无摩擦的市场中，资产价格的变化符合Ito过程，在这种条件下，资产的价格与投资者的效用偏好无关。在随后的研究中Merton(1973)和Black(1973)应用以上连续时间模型成功地得到了期权定价公式，这一公式后来被大量的实证研究所证实，并且被广泛在实践中应用。

　　传统CAPM中的一个关键假设是投资者只考虑单一投资期，很显然这是一个不现实的假设。为了放松这一假设，把CAPM模型扩展到动态环境中，默顿(1969,1972,1973)构建了一个连续时间的投资组合与资产定价的理论框架，提出了一个跨期CAPM (ICAPM)。

　　默顿认为，投资者对风险证券的需求包括两部分：马科维茨的静态资产组合最优化问题中的均值一方差成分和规避对投资机会集的不利冲击的需求。当投资机会集发生不利变动，而同时又存在一种收益率很高的证券时，每一个理性的投资者都会希望买入该种证券作为一种套期保值措施。这种套期保值需求的增加同时也导致了该证券均衡价格的升高，推导ICAPM的关键就是在资产定价方程中反映这种套期保值需求。

　　在ICAPM中，投资者的决策将最大化整个投资期的效用，即：

　　其中，U^k表示投资者k的效用，C^k表示投资者k的消费，\rho表示未来效用的贴现因子。第一项表示从0到T期的消费效用的现值，第二项表示在T期末财富效用的现值。

　　按照动态规划原理，求解上述最大化问题需要确定每一期的消费量Ck(t)和余下财富投资于每一资产的比重Wk(t)ni=1。为此，定义一个性能函数Jk(Wk,t,X)为：

　　利用高等数学和随机微分知识，可求得(n+1)个最大化的一阶条件，由此可以确定投资者在每一期的消费和投资组合变量。进一步地，默顿提出了类似于托宾分离定理的"（m+2）基金定理"(其中，m表示状态变量个数)。他认为投资者应该持有(m+2)个资产组合：（1）最优风险证券组合，即切点组合；(2)无风险资产组合；（3）与某一状态变量高度负相关的资产构成的其他m个资产组合(即套期保值组合)。前两个资产组合确保投资者持有均值方差有效的资产组合，即位于静态CAPM的有效边界上，后m个资产组合则是为规避投资机会集的不利变动。

　　对所有投资者的需求方程加总，利用均衡状态下总需求等于所有资产的总价值的基本原理，最终可推导出跨期资本资产定价模型ICAPM：

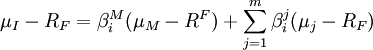
　　在ICAPM中，即使β值为零的资产，即与市场组合不相关的资产，其收益率也可能高于无风险利率，因为还需补偿状态变量的不利变动风险暴露。