鞅定价方法发表评论(0) 编辑词条

鞅定价方法(Martingale Pricing Technique/martingale pricing theory/theory of martingale pricing)

　　Harrison 及 Kreos (1979)提出了一种求解金融衍生产品的定价方法——鞅定价方法。在鞅定价方法下，证券的价格可由折现该产品未来现金流量得到，且期望值折现在风险中立下计算。鞅定价方法比随机微分方程简单，也不会涉及复杂的积分。许多随机微分方程不能求解的问题，鞅定价方法可轻易求解。

　　股票价格的随机过程可以表示为：

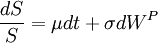
　　 $\frac{dS}{S}=\mu dt+\sigma dW^P$

　　 $W P$ 表示在概率测度P下的布朗运动。上述公式可以转化为风险中性概率测度Q下的随机过程：

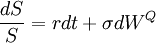
　　 $\frac{dS}{S}=rdt+\sigma dW^Q$

　　其中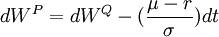： $dW^P=dW^Q-(\frac{\mu-r}{\sigma})dt$ 。

　　比较上述两个公式可以发现，原来的μ已经被无风险利率r 取代，波动率σ 并未受到影响。

　　在风险中性概率测度Q下，股票价格的动态过程变为：

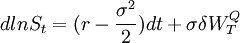
　　 $d lnS_t=(r-\frac{\sigma^2}{2})dt+\sigma\delta W^Q_T$

　　因此，相应的其动态过程可表示为：

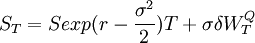
　　 $S_T=S exp(r-\frac{\sigma^2}{2})T+\sigma\delta W^Q_T$

　　在定价股票期权时，须计算 $E Q [S T | S T > K]$ ，它表示在到期日T，股价S_T大于执行价格K 的期望。

　　利用Girsanov 定理，经过一系列推导，可以得到：

　　 $E Q [S T | S T > K] = S E r T N (d 1)$

　　其中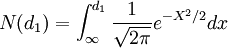， $N(d_1)=\int_{\infty}^{d_1}\frac{1}{\sqrt{2\pi}}e^{-X^2/2}dx$ 标准正态分布的累积概率。

　　计算出 $E Q [S T | S T > K]$ 后，然后再依据买、卖权以及其它相应的条件比较容易的得到股票期权的价格。

→如果您认为本词条还有待完善，请编辑词条

词条内容仅供参考，如果您需要解决具体问题
（尤其在法律、医学等领域），建议您咨询相关领域专业人士。本词条对我有帮助2

收藏到:

同义词: 暂无同义词

关于本词条的评论 (共0条）发表评论>>

鞅定价方法 发表评论(0) 编辑词条