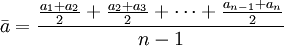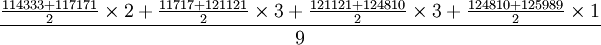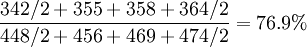平均发展水平 发表评论(0) 编辑词条
平均发展水平(Average level of development)
什么是平均发展水平 编辑本段回目录
平均发展水平又称“序时平均数”、“动态平均数”,是时间序列中各项发展水平的平均数,反映现象在一段时期中发展的一般水平。
序时平均数作为一种平均数,与静态平均数有相同点,即它们都抽象了现象的个别差异,以反映现象总体的一般水平。但二者又有明显的区别,主要表现在:序时平均数抽象的是现象在不同时间上的数量差异,因而它能够从动态上说明现象在一定时期内发展变化的一般趋势;静态平均数抽象的是总体各单位某一数量标志值在同一时间上的差异,因此,它是从静态上说明现象总体各单位的一般水平。由于不同时间序列中观察值的表现形式不同,序时平均数有不同的计算方法。
平均发展水平的计算 编辑本段回目录
(一)绝对数时间数列的序时平均数
绝对数时间数列序时平均数的计算方法是最基本的,它是计算相对数或平均数时间数列序时平均数的基础。绝对数时间数列有时期数列和时点数列之分,序时平均数的计算方法也有所区别。
1、时期数列的序时平均数,其计算公式为:
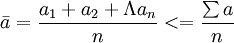 (1)
(1)
式中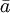 为序时平均数,n为观察值的个数。
为序时平均数,n为观察值的个数。
例1:对表1中的国内生产总值序列,计算年度平均国内生产总值。
表1 中国国内生产总值等时间序列表
| 年份 | 国内生产总值(亿元) | 第三产业占GDP比重(%) | 年底总人口(万人) | 职工平均货币工资(元) |
|---|---|---|---|---|
| 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 | 18547.9 21617.9 26638.1 34634.4 46759.4 58478.1 67884.6 74462.6 78345.2 81910.9 | 31.3 33.4 34.3 32.7 31.9 30.7 30.1 30.9 32.1 33.0 | 114333 115823 117171 118517 119850 121121 122889 123626 124810 125909 | 2140 2340 2711 3371 4538 5500 6210 6470 7479 8346 |
资料来源:《中国统计年鉴》,中国统计出版社,2001年
解:根据时期数列序时平均数公式有:
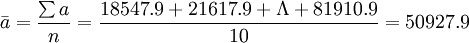 (亿元)
(亿元)
2、由时点数列计算序时平均数。在社会经济统计中一般是将一天看作一个时点,即以“一天”作为最小时间单位。这样时点数列可认为有连续时点和间断时点数列之分;而间断时点数列又有间隔相等与间隔不等之别。其序时平均数的计算方法略有不同,分述如下:
1)连续时点数列计算序时平均数。在统计中,对于逐日排列的时点资料,视其为连续时点资料。这样的连续时点数列,其序时平均数公式可按公式(1)计算,即
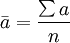 (2)
(2)
例如,存款(贷款)平均余额指标,通常就是由报告期内每日存款(贷款)余额之和除以报告期日历数而求得。
另一种情形是,资料登记的时间单位仍然是1天,但实际上只在指标值发生变动时才记录一次。此时需采用加权算术平均数的方法计算序时平均数,权数是每一指标值的持续天数。
计算公式如下:
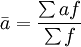
例2:某种商品5月份的库存量记录如表2,计算5月份平均日库存量。
表2 某种商品5月份库存资料
| 日期 | 1-4 | 5-10 | 8–20 | 21-26 | 27-31 |
|---|---|---|---|---|---|
| 库存量(台) | 50 | 55 | 40 | 35 | 30 |
解:该商品5月份平均日库存量为
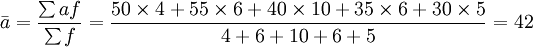 (台)
(台)
2)间断时点数列计算序时平均数。实际统计工作中,很多现象并不是逐日对其时点数据进行统计,而是隔一段时间(如一月、一季度、一年等)对其期末时点数据进行登记。这样得到的时点数列称为间断时点数列。如果每隔相同的时间登记一次,所得数列称为间隔相等的间断时点数列;如果每两次登记时间的间隔不尽相同,所得数列称为间隔不等的间断时点数列。
当其时点资料是以月度、季度、年度为时间间隔单位,我们已不可能像连续时点资料那样求得准确的时点平均数。这种情况下,我们可以根据资料所属时间的间隔特点,选用不同的计算公式。对于间隔相等的资料,采用“首末折半”;对于间隔不等的资料,采用“间隔加权”的方法计算序时平均数。
例3:某商业企业1999年第二季度某种商品的库存量如表3,试求该商品第二季度月平均库存量。
表3 某商业企业1999年第二季度某商品库存量
| 3月末 | 4月末 | 5月末 | 6月末 | |
|---|---|---|---|---|
| 库存量(百件) | 66 | 72 | 64 | 68 |
- 解:4月份平均库存量=
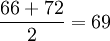 (百件)
(百件)
- 5月份平均库存量=
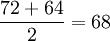 (百件)
(百件)
- 6月份平均库存量=
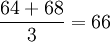 (百件)
(百件)
- 第二季度平均库存量
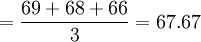 (百件)
(百件)
为简化计算过程,上述计算步骤可表示为:
第二季度平均库存量=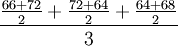 =
=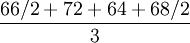 =67.67(百件)
=67.67(百件)
根据上述计算过程可推导出计算公式为:
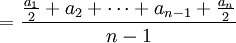 (4)
(4)
该公式形式上表现为首末两项观察值折半,故称为“首末折半法”。这种方法适用于间隔相等的间断时点数列求序时平均数。
例4:表4列示了我国1990~1999年年末人口的部分年份资料,计算年平均人口数。
表4 中国1990-1999年部分年份年末人口数
| 年份 | 1990 | 1992 | 1995 | 1998 | 1999 |
|---|---|---|---|---|---|
| 年底总人口(万人) | 114333 | 117171 | 121121 | 124810 | 125909 |
解:对资料进行观察分析,属间隔不等的间断时点资料,采用“间隔加权”方法。
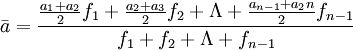 (5)
(5)
- =120355.33(万人)
(二)相对数或平均数时间数列的序时平均数
相对数和平均数是两个有联系的相对数对比求得,用符号表示即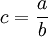 。因此,由相对数或平均数数列计算序时平均数,不能直接根据该相对数或平均数数列中各项观察值简单平均计算(即不应当用
。因此,由相对数或平均数数列计算序时平均数,不能直接根据该相对数或平均数数列中各项观察值简单平均计算(即不应当用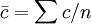 的公式),而应当先分别计算构成该相对数或平均数数列的分子数列和分母数列的序时平均数,再对比求得。用公式表示为:
的公式),而应当先分别计算构成该相对数或平均数数列的分子数列和分母数列的序时平均数,再对比求得。用公式表示为:
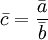 (6)
(6)
例5:某企业1999年第四季度职工人数资料如表5,计算工人占职工人数的平均比重。
表5 某企业1999年四季度职工人数资料
| 9月末 | 10月末 | 11月末 | 12月末 | |
| 工人人数/人 职工人数/人 工人占职工比重/% | 342 448 76.34 | 355 456 77.85 | 358 469 76.33 | 364 474 76.79 |
解:
参考文献编辑本段回目录
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
1
标签: 平均发展水平 加权算术平均数 发展水平 国内生产总值 平均数 时期数列 时点数列 时间序列 相对数 绝对数时间数列 统计

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条