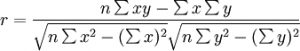相关系数 发表评论(0) 编辑词条
相关系数(Correlation coefficient)
什么是相关系数编辑本段回目录
相关表和相关图可反映两个变量之间的相互关系及其相关方向,但无法确切地表明两个变量之间相关的程度。
著名统计学家卡尔·皮尔逊设计了统计指标——相关系数。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
依据相关现象之间的不同特征,其统计指标的名称有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数(相关系数的平方称为判定系数);将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数;将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。
相关系数的公式编辑本段回目录
相关系数用r表示,它的基本公式为:
相关系数的值介于–1与+1之间,即–1≤r≤+1。其性质如下:
当r>0时,表示两变量正相关,r<0时,两变量为负相关。
当|r|=1时,表示两变量为完全线性相关,即为函数关系。
当r=0时,表示两变量间无线性相关关系。
当0<|r|<1时,表示两变量存在一定程度的线性相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
一般可按三级划分:|r|<0.4为低度线性相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关。
例:某财务软件公司在全国有许多代理商,为研究它的财务软件产品的广告投入与销售额的关系,统计人员随机选择10家代理商进行观察,搜集到年广告投入费和月平均销售额的数据,并编制成相关表,见表1:
表1 广告费与月平均销售额相关表 单位:万元
年广告费投入月均销售额
| 12.5 | 21.2 |
| 15.3 | 23.9 |
| 23.2 | 32.9 |
| 26.4 | 34.1 |
| 33.5 | 42.5 |
| 34.4 | 43.2 |
| 39.4 | 49.0 |
| 45.2 | 52.8 |
| 55.4 | 59.4 |
| 60.9 | 63.5 |
参照表1,可计算相关系数如表2:
序号广告投入(万元)x月均销售额(万元)
yx^2y2xy
| 1 2 3 4 5 6 7 8 9 10 |
12.5 15.3 23.2 26.4 33.5 34.4 39.4 45.2 55.4 60.9 |
21.2 23.9 32.9 34.1 42.5 43.2 49.0 52.8 59.4 63.5 |
156.25 234.09 538.24 696.96 1122.25 1183.36 1552.36 2043.04 3069.16 3708.81 |
449.44 571.21 1082.41 1162.81 1806.25 1866.24 2401.00 2787.84 3528.36 4032.25 |
265.00 365.67 763.28 900.24 1423.75 1486.08 1930.60 2386.56 3290.76 3867.15 |
| 合计 | 346.2 | 422.5 | 14304.52 | 19687.81 | 16679.09 |

相关系数为0.9942,说明广告投入费与月平均销售额之间有高度的线性正相关关系。
各种相关系数介绍与对比 编辑本段回目录
按照变量的不同测量层次对各种相关系数简单介绍:
1、 定类变量——定类变量 用于测量两个定类变量的相关系数,主要有Lambda 与Tau-y两种。
(1)Lambda(λ)系数分为:对称形式——用于测量两个变量间的关系是对等的,即无自变量与因变量之分。非对称形式——测量两个变量间的关系有自变量与因变量之分。
(2) Tau-y系数:用于测量变量间非对称关系的。
2、 定序变量——定序变量 如果测量两个定序尺度变量间的关系,可用Gamma系数、dyx系数和斯皮尔曼等级相关系数。
(1) Gamma(G)系数:分析两个变量间的对等关系,即无自变量与因变量之分。
(2) dyx系数:等级相关系数,两个变量间的关系是非对称的。
(3) 斯皮尔曼(Spearman)等级相关系数(ρ):考虑单个个案在两个变量上的等级差异,测量两变量间对等相关关系。
3、 定距变量——定距变量
测量两个定距变量相关系数的最常用指标是皮尔森(Pearson)相关系数(γ)。(要求N≥50而且两个变量的分布应近似于正态分布。)
4、 定类变量——定距变量 两个变量中,自变量为定类变量,因变量为定距变量时,采用相关比率来测量两者间相关程度。(又称eta平方系数E)
5、 定类变量——定序变量
对一个定类变量例如性别,与一个定序变量例如收入水平关系的分析:第一,用theta系数(θ),专门测量定类变量与定序变量间关系有无和强度,非对称关系。第二,采用λ系数和Tau-y系数,即将定序变量作为定类变量处理。
6、 定序变量——定距变量 处理一个定序变量例如教育水平,与一个定距变量如年均收入之间的关系,采用二种办法:
第一, 将定序变量看作定类变量,采用相关比例测量法。
第二, 将定序变量看作定距变量,采用γ相关系数。
小结:在分析两个变量关系时,选择哪种相关系数,主要考虑两个方面:
1、 变量的测量层次;
2、 变量关系的类别,即是对等的还是非对称的。
相关系数的缺点编辑本段回目录
需要指出的是,相关系数有一个明显的缺点,即它接近于1的程度与数据组数n相关,这容易给人一种假象。因为,当n较小时,相关系数的波动较大,对有些样本相关系数的绝对值易接近于1;当n较大时,相关系数的绝对值容易偏小。特别是当n=2时,相关系数的绝对值总为1。因此在样本容量n较小时,我们仅凭相关系数较大就判定变量x与y之间有密切的线性关系是不妥当的。
例如,就我国深沪两股市资产负债率与每股收益之间的相关关系做研究。发现1999年资产负债率前40名的上市公司,二者的相关系数为r=–0.6139;资产负债率后20名的上市公司,二者的相关系数r=0.1072;而对于沪、深全部上市公司(基金除外)结果却是,r沪=–0.5509,r深=–0.4361,根据三级划分方法,两变量为显著性相关。这也说明仅凭r的计算值大小判断相关程度有一定的缺陷。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
4

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条