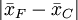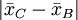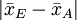HSD检验法 发表评论(0) 编辑词条

　　J·W·图凯（Tukey）于1953年提出一种能将所有各对平均值同时比较的方法，这种方法现在已被广泛采用，一般称之为“HSD检验法”，或称“W法”。

　　采用图凯检验法时，只要计算一个数值，就能借以完成所有各对平均值之差的比较。这个数值称为HSD，由以下公式给出：

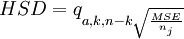
　　其中的q值与显著性水平α，实验中平均值的个数k以及误差自由度n-k有关，可由附表H查出。任何一对平均值之差只要超过HSD值，就表明这一对平均值之间的差别是显著的。注意，统计量HSD要求所有样本的容量都相等，即要求n₁ = n₂ = Λ = n_j。

　　让我们举例来说明这种方法的应用。

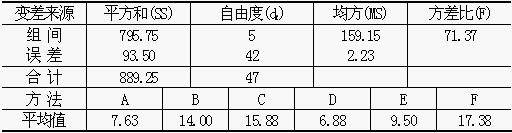
　　为了对生产某种化合物的6种方法作比较，进行了一项实验，得到的数据列于表1。感兴趣的变量是这种化合物中固体物质的含量百分比。每种方法都有8个观察值。假定在显著性水平α=0.05之下，通过方差分析所算出的F是显著的。现在，产生的合乎逻辑的问题恰好就是什么地方出现了显著差别的问题。

　　　　　　　　　　方差分析表

　　解：图凯检验法能为这个问题提供答案。

　　在把图凯的HSD方法应用于表1中的数据之前，我们先把各对平均值之差的绝对值列成表2。表中行和列中的样本处理平均值均按由大到小的数值顺序排列，表中给出相应的差值。

　　　　　　　　　　诸平均值之差的绝对值

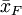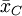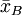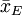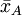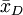
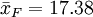	-	1.50	3.38	7.88	9.75	10.50
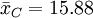		-	1.88	6.38	8.25	9.00
			-	4.50	6.37	7.12
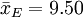				-	1.87	2.62
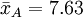					-	0.75
						-

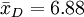　　如果选择显著性水平α=0.05，便可从附表H查出q_0.05,6,42 = 4.22(自由度可在40与60之间作内插)。从表1可找到MSE=2.23，于是，算出：

　　当我们将表2中各种平均值之差同2.23比较时，发现只有以下几对平均值之差不显著：

　　其余差值都是显著的。