威尔科克森符号秩检验 发表评论(0) 编辑词条
威尔科克森符号秩检验（Wilcoxon's Sign Rank Test）
什么是威尔科克森符号秩检验[1] 编辑本段回目录
威尔科克森符号秩检验是由威尔科克森（F·Wilcoxon）于1945年提出的。该方法是在成对观测数据的符号检验基础上发展起来的，比传统的单独用正负号的检验更加有效。它适用于T检验中的成对比较，但并不要求成对数据之差di服从正态分布，只要求对称分布即可。检验成对观测数据之差是否来自均值为0的总体（产生数据的总体是否具有相同的均值）。
威尔科克森符号秩检验的步骤[1] 编辑本段回目录
正负符号检验和威尔科克森符号秩检验，都可看作是就成对观察值而进行的参数方式的T检验的代用品，非参数检验具有无需对总体分布作假定的优点，而就成对观察值作的参数方式的T检验，必须假定有关的差别总体服从正态分布。
该方法具体步骤如下：
第一步：求出成对观测数据的差di，并将di的绝对值按大小顺序编上等级（曼-惠特尼U检验）。
第二步：等级编号完成以后恢复正负号，分别求出正等级之和T+和负等级之和T-，选择T+和T-中较小的一个作为威尔科克森检验统计量T。
第三步；作出判断。
根据显著性水平α查附表，得到临界值Tα，若T＜Tα，则拒绝原假设H0。当观测值不少于20对时，统计量T的均值和方差分别为：
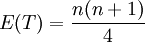
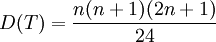(n为成对观测的个数)
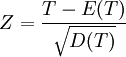(近似服从标准正态分布)
若Z＜-Zα(单侧)或Z＜-Zα/2(双侧)，则拒绝H0。
威尔科克森符号秩检验的应用举例[1] 编辑本段回目录
下面是分别用高锰酸钾法和EDTA法对某生长期蛋鸡配合料钙含量进行的7次测定结果(湖北省饲料质量监督检验站2002年常规检测样品)，比较两种方法测定结果差异是否显著。
首先按大小顺序对两对观测值之差di进行等级排序，并加上正负号，分别计算正负等级之和：T+=21，T-=-7。
高锰酸钾法和EDTA法测定蛋鸡配合料钙含量结果(%)
| 编号 | 高锰酸钾法 | EDTA法 | di | 等级 |
|---|---|---|---|---|
| 1 | 1.26 | 1.24 | 0.02 | 4.5 |
| 2 | 1.24 | 1.28 | -0.04 | -7 |
| 3 | 1.24 | 1.21 | 0.03 | 6 |
| 4 | 1.25 | 1.25 | 0 | 1.5 |
| 5 | 1.26 | 1.26 | 0 | 1.5 |
| 6 | 1.25 | 1.24 | 0.01 | 3 |
| 7 | 1.24 | 1.22 | 0.02 | 4.5 |
假设两种方法检测饲料中钙含量结果无显著差异，即检验：
- H0：两种方法检测结果无显著差异；
- H1：两种方法检测结果有差异。
查附表得到，对于α=0.05的双侧检验，n=7 时，T0.025=2。由于 T+=21＞ T0.025 ，则接受H0，可以认为两种方法测定饲料钙含量结果并无显著差异。
附表
威尔科克森带符号秩检验T的临界值表
| 单侧α | 双侧α | n值 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.10 | T值 | 1 | 2 | 4 | 6 | 8 | 11 | 14 | 17 | 21 | 26 | 30 | 36 |
| 0.025 | 0.05 | 1 | 2 | 4 | 6 | 8 | 11 | 14 | 17 | 21 | 25 | 30 | ||
| 0.01 | 0.02 | 0 | 2 | 3 | 5 | 7 | 10 | 13 | 16 | 20 | 24 | |||
| 0.005 | 0.01 | 0 | 2 | 3 | 5 | 7 | 10 | 13 | 16 | 19 |
参考文献 编辑本段回目录
附件列表
→如果您认为本词条还有待完善，请 编辑词条
词条内容仅供参考，如果您需要解决具体问题
（尤其在法律、医学等领域），建议您咨询相关领域专业人士。
0
标签: 威尔科克森符号秩检验 T检验 方差 曼-惠特尼U检验 正态分布 符号检验 统计量 威尔科克森
同义词: 暂无同义词
关于本词条的评论 (共0条）发表评论>>
