Z检验 发表评论(0) 编辑词条

Z检验（Z Test）

　　Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。

　　当已知标准差时，验证一组数的均值是否与某一期望值相等时，用Z检验。

　　第一步：建立虚无假设，即先假定两个平均数之间没有显著差异，

　　第二步：计算统计量Z值，对于不同类型的问题选用不同的统计量计算方法，

　　1、如果检验一个样本平均数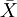（）与一个已知的总体平均数(μ₀)的差异是否显著。其Z值计算公式为：

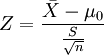
　　其中：

• 是检验样本的平均数；
• μ₀是已知总体的平均数；
• S是样本的标准差；
• n是样本容量。

　　2、如果检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为：

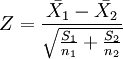
　　其中：

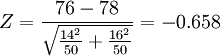• 是样本1，样本2的平均数；
• S₁,S₂是样本1，样本2的标准差；
• n₁,n₂是样本1，样本2的容量。

　　第三步：比较计算所得Z值与理论Z值，推断发生的概率，依据Z值与差异显著性关系表作出判断。如下表所示：

　　第四步：根据是以上分析，结合具体情况，作出结论。

　　某项教育技术实验，对实验组和控制组的前测和后测的数据分别如下表所示，比较两组前测和后测是否存在差异。

实验组和控制组的前测和后测数据表
前测	实验组	n1 = 50		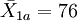S1a = 14
	控制组	n2 = 48		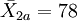S2a = 16
后测	实验组	n1 = 50		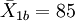S1b = 8
	控制组	n2 = 48		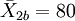S2b = 14

　　由于n＞30，属于大样本，所以采用Z检验。由于这是检验来自两个不同总体的两个样本平均数，看它们各自代表的总体的差异是否显著，所以采用双总体的Z检验方法。

　　计算前测Z的值：

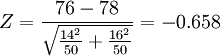
∵|Z|=0.658＜1.96

∴ 前测两组差异不显著。

　　再计算后测Z的值:

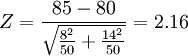
∵|Z|= 2.16＞1.96

∴ 后测两组差异显著。