抽样误差 发表评论(0) 编辑词条
抽样误差(Sampling error)
什么是抽样误差 编辑本段回目录
在抽样检查中,由于用样本指标代替全及指标所产生的误差可分为两种:一种是由于主观因素破坏了随机原则而产生的误差,称为系统性误差;另一种是由于抽样的随机性引起的偶然的代表性误差。抽样误差仅仅是指后一种由于抽样的随机性而带来的偶然的代表性误差,而不是指前一种因不遵循随机性原则而造成的系统性误差。
总的说来,抽样误差是指样本指标与全及总体指标之间的绝对误差。在进行抽样检查时不可避免会产生抽样误差,因为从总体中随机抽取的样本,其结构不可能和总体完全一致。例如样本平均数与总体平均数之差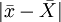 ,样本成数与总体成数之差 | p − P | 。虽然抽样误差不可避免,但可以运用大数定律的数学公式加以精确地计算,确定它具体的数量界限,并可通过抽样设计加以控制。
,样本成数与总体成数之差 | p − P | 。虽然抽样误差不可避免,但可以运用大数定律的数学公式加以精确地计算,确定它具体的数量界限,并可通过抽样设计加以控制。
抽样误差也是衡量抽样检查准确程度的指标。抽样误差越大,表明抽样总体对全及总体的代表性越小,抽样检查的结果越不可靠。反之,抽样误差越小,说明抽样总体对全及总体的代表性越大,抽样检查的结果越准确可靠。在统计学中把抽样误差分为抽样平均误差和抽样极限误差,下面就这两种误差分别进行阐释。为使推理过程简化,这里不对属性总体进行分析,而仅对变量总体进行分析计算。
抽样误差的计算 编辑本段回目录
1、表现形式:平均数指标抽样误差;成数(比重)抽样误差。
2、平均数指标的抽样误差
1)重复抽样的条件下:
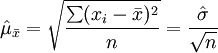
2)不重复抽样的条件下:
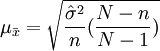
3、成数指标的抽样误差
1)重复抽样的条件下:
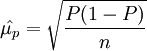
2)不重复抽样的条件下:
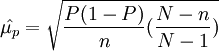
抽样误差的控制措施 编辑本段回目录
抽样误差则是不可避免的,但可以减少,其措施有:
1、增加样本个案数。
2、适应选择抽样方式。
例如,在同样条件下,又重复抽样比重复抽样的抽样误差小,又如在总体现象分类比较明显时,采用分层随机抽样比其它方法的抽样误差小。由于总体真正的参数值未知,真正的抽样误差也未知,所以抽样误差的计算一般都以抽样平均误差来代表真正的抽样误差。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 抽样误差 不重复抽样 全及总体 全及指标 分层随机抽样 大数定律 总体 抽样平均误差 抽样总体 抽样极限误差 抽样检查

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条

