四分位数 发表评论(0) 编辑词条
四分位数(Quartile)
什么是四分位数 编辑本段回目录
分位数根据其将数列等分的形式不同可以分为中位数,四分位数,十分位数、百分位数等等。四分位数作为分位数的一种形式,在统计中有着十分重要的意义和作用。
人们经常会将数据划分为4个部分,每一个部分大约包含有1/4即25%的数据项。这种划分的临界点即为四分位数。它们定义如下:
- Q1=第1四分位数,即第25百分位数;
- Q2=第2四分位数,即第50百分位数;
- Q3=第3四分位数,即第75百分位数。
四分位数的计算 编辑本段回目录
(一)根据未分组的资料计算四分位数
第一步:确定四分位数的位置。
四分位数是将数列等分成四个部分的数,一个数列有三个四分位数,设下四分位数、中位数和上四分位数分别为Q1、Q2、Q3,则:Q1、Q2、Q3的位置可由下述公式确定:
Q1的位置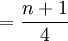
Q2的位置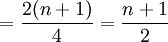
Q3的位置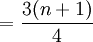
式中n表示资料的项数
第二步:根据第一步所确定的四分位数的位置,确定其相应的四分位数。
例如:某车间某月份的工人生产某产品的数量分别为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4、15.7公斤,则三个四分位数的位置分别为:
Q1的位置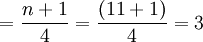
Q2的位置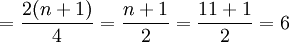
Q3的位置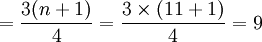
即变量数列中的第三个、第六个、第九个工人的某种产品产量分别为下四分位数、中位数和上四分位数。即:
Q1 = 13.8公斤、Q2 = 14.6公斤、Q3 = 15.2公斤
上例中(n+1)恰好为4的倍数,所以确定四分数较简单,如果(n+1)不为4的整数倍数,按上述分式计算出来的四分位数位置就带有小数,这时,有关的四分位数就应该是与该小数相邻的两个整数位置上的标志值的平均数,权数的大小取决于两个整数位置距离的远近,距离越近,权数越大,距离越远,权数越小,权数之和等于1。
例如:某车间某月份的工人生产某产品的数量分别为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4公斤,则三个四分位数的位置分别为:
Q1的位置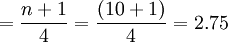
Q2的位置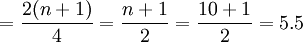
Q3的位置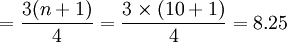
即变量数列中的第2.75项、第5.5项、第8.25项工人的某种产品产量分别为下四分位数、中位数和上四分位数。即:
Q1=0.25×第二项+0.75×第三项=0.25×13.5+0.75×13.8=13.73(公斤)
Q2=0.5×第五项+0.5×第六项=0.5×14+0.5×14.6=14.3(公斤)
Q3=0.75×第八项+0.25×第九项=0.75×15+0.25×15.2=15.05(公斤)
在实际资料中,由于标志值序列中的相邻标志值往往是相同的,因而不一定要通过计算才能得到有关的四分位数。
(二)由组距式数列确定四分位数
第一步,向上或向下累计次数。
第二步,根据累计次数确定四分位数的位置。
1)当采用向上累计次数的资料确定四分位数时,四分位数位置的公式是:
Q1的位置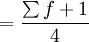
Q2的位置
Q3的位置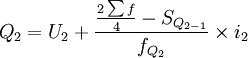
式中: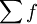 表示资料的总次数。
表示资料的总次数。
2)当采用向下累计次数的资料确定四分位数时,四分位数位置的公式是:
Q1的位置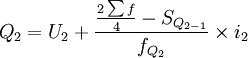
Q2的位置
Q3的位置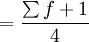
式中: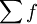 表示资料的总次数。
表示资料的总次数。
第三步,根据四分位数的位置算出各四分位数。
1)当累计次数是向上累计时,按下限公式计算各四分位数。
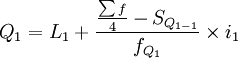
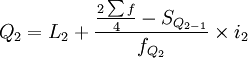
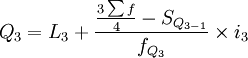
式中:Q1、Q2、Q3分别表示下四分位数、中位数和上四分位数;
L1、L2、L3分别表示下四分位数、中位数和上四分位数所在组的下限;
i1、i2、i3分别表示下四分位数、中位数和上四分位数所在组的组距;
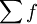 表示总次数;
表示总次数;
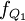 、
、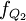 、
、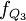 分别表示下四分位数、中位数和上四分位数所在组的次数;
分别表示下四分位数、中位数和上四分位数所在组的次数;
SQ1 − 1表示下四分位数前一组的累计次数;
SQ2 − 1表示中位数前一组的累计次数;
SQ3 − 1表示上四分位数前一组的累计次数。
2)当累计次数是向下累计时,按上限公式计算各四分位数。
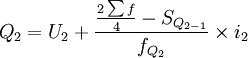
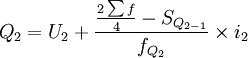
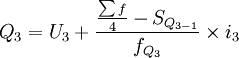
式中:Q1、Q2、Q3分别表示下四分位数、中位数和上四分位数;
U1、U2、U3分别表示下四分位数、中位数和上四分位数所在组的上限;
i1、i2、i3分别表示下四分位数、中位数和上四分位数所在组的组距;
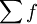 表示总次数;
表示总次数;
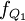 、
、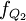 、
、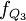 分别表示下四分位数、中位数和上四分位数所在组的次数;
分别表示下四分位数、中位数和上四分位数所在组的次数;
SQ1 − 1表示下四分位数后一组的累计次数;
SQ2 − 1表示中位数后一组的累计次数;
SQ3 − 1表示上四分位数后一组的累计次数。
例如:某企业职工按月工资的分组资料如下:
| 按月工资分组(元) | 职工人数(人) | 向上累计职工人数 | 向下累计职工人数 |
|---|---|---|---|
| 600以下 | 23 | 23 | 566 |
| 600—700 | 120 | 143 | 543 |
| 700—800 | 150 | 293 | 423 |
| 800—900 | 135 | 428 | 273 |
| 900—1000 | 95 | 523 | 138 |
| 1000以上 | 43 | 566 | 43 |
| 合计 | 566 | —— | —— |
根据上述资料确定某企业职工的月工资的三个四分位数如下:
1)采用向上累计职工人数的资料得月工资四分位数的位置为:
Q1的位置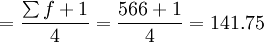
Q2的位置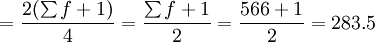
Q3的位置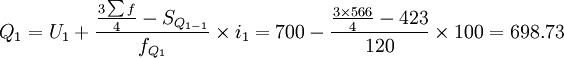
根据计算结果可知,Q1、Q2、Q3分别位于向上累计职工人数的第二组、第三组和第 四组,月工资四分位数分别为:
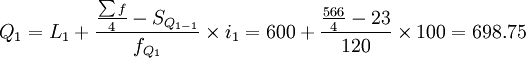 (元)
(元)
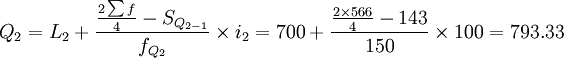 (元)
(元)
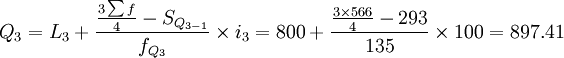 (元)
(元)
2)采用向下累计职工人数的资料得月工资四分位数的位置为:
Q1的位置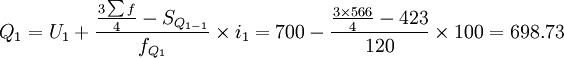
Q2的位置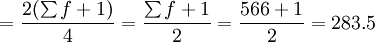
Q3的位置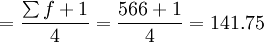
同样可知:Q1、Q2、Q3分别位于向下累计职工人数的第二组、第三组和第四组,月 工资四分位数分别为:
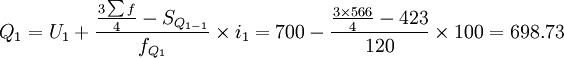 (元)
(元)
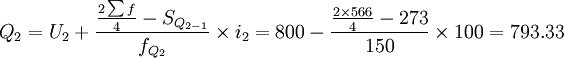 (元)
(元)
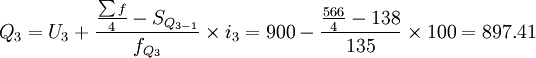 (元)
(元)
计算结果同按下限公式计算的一致,即所求某企业职工月工资的三个四分数也分别为698.75元、793.33元和897.41元。
四分位数举例 编辑本段回目录
下面是按递增顺序排列的起始月薪数据。Q2即第2四分位数(中位数),已被确知为2405。
- 2210 2255 2350 2380 2380 2390 2420 2440 2450 2550 2630 2825
计算Q1和Q3需要用到计算第25百分位数和第75百分位数的方法。它们的计算如下:
- 对Q1:i=(p/100)×n=(25/100)×12=3
由于i为整数,由第3步的(2)可知,第1四分位数即第25百分位数即为第3项与第4项的平均值。所以Q1=(2350+2380)/2=2365。
- 对Q3:i=(p/100)×n=(75/100)×12=9
同样i为整数,由第3步的(2)可知,第3四分位数即第75百分位数即为第9项与第10项的平均值。所以Q3=(2450+2550)/2 =2500。
如下所示,四分位数将12个数据分为了4个部分,每个部分含有25%的数据项。
- 2210 2255 2350 | 2380 2380 2390 | 2420 2440 2450 | 2550 2630 2825
- Q1=2365 Q2=2405 Q3=2500
- (中位数)
我们已将四分位数分别定义为第25、50、75百分位数。因此,四分位数的计算方法与其他百分位数的计算方法是相同的。但是在计算四分位数时有些方法的约定是不同的;而计算出来的值也会因这些约定的不同而稍有差异。尽管如此,无论采用何种计算过程,计算四分位数的目的都是将数据划分为大致相等的4个部分。
参考文献 编辑本段回目录
- 论四分位数的计算.作者:祁德军,陈明
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 四分位数 中位数 变量数列 平均数 百分位数 统计 分位数 十分位数

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条

