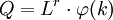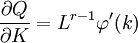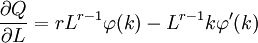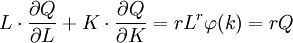欧拉定理 发表评论(0) 编辑词条
欧拉定理(Euler Theorem),也称费马-欧拉定理或欧拉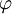 函数定理
函数定理
什么是欧拉定理 编辑本段回目录
欧拉定理指出:如果产品市场和要素市场都是完全竞争的,而且厂商生产的规模报酬不变,那么在市场均衡的条件下,所有生产要素实际所取得的报酬总量正好等于社会所生产的总产品。该定理又叫做边际生产力分配理论,还被称为产品分配净尽定理。如上所述,要素的价格是由于要素的市场供给和市场需求共同决定。在完全竞争的条件下,厂商和消费者都被动地接受市场形成的价格。现在的问题是:要素所有者按照市场形成的要素价格获得收入,全部要素收入是否等于社会总产品?
在完全竞争的条件下,厂商使用要素的原则是:要素的边际产品价值等于要素价格。即:
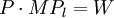 (9.9)
(9.9)
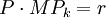 (9.10)
(9.10)
由式9.9和9.10可得:
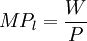 (9.11)
(9.11)
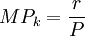 (9.12)
(9.12)
P为产品的价格,W/P和r/P分别表示了劳动和资本的实际报酬。因此在完全竞争的条件下,单位劳动、单位资本的实际报酬分别等于劳动、资本的边际产量。假定整个社会的劳动总量和资本总量为L和K,而社会总产品为Q,那么就有:
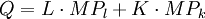 (9.13)
(9.13)
式9.13称为欧拉分配定理。它是由于该定理的证明使用了数学上的欧拉定理而得名。
欧拉定理的证明 编辑本段回目录
本词条由以下会员参与贡献
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
20
标签: 欧拉定理 生产函数 生产要素 社会总产品 规模报酬递增 边际产品价值 边际产量
收藏到: 

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
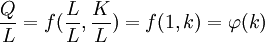
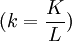
![{\partial Q \over \partial L} = {{\partial [ L \cdot \varphi (k) ] } \over \partial L} = \varphi (k) + L \cdot {{d \varphi (k) } \over dk} \cdot {dk \over dL} = \varphi (k) + L \cdot \varphi ^\prime (k) \cdot {dk \over dL} = \varphi (k) + L \cdot \varphi ^\prime (k) \cdot \left( {{-K } \over {L^2} } \right) = \varphi (k) - k \cdot \varphi ^\prime (k)](Article/UploadFiles/200908/2009082109075903.png)
![{\partial Q \over \partial K} = {{\partial [ L \cdot \varphi (k) ] } \over \partial K} = L \cdot {{\partial \varphi (k)} \over \partial k } = L \cdot {{d \varphi (k) } \over dk} \cdot {{\partial k} \over {\partial K}} = L \cdot \varphi ^\prime (k) \cdot {1 \over L } = \varphi ^\prime (k)](Article/UploadFiles/200908/2009082109080048.png)
![L \cdot {\partial Q \over {\partial L}} + K \cdot {{\partial Q } \over {\partial K}} = L \cdot [\varphi (k) - k \varphi ^\prime (k)] + K \cdot \varphi ^\prime (k) = L \cdot \varphi (k) - K \cdot \varphi ^\prime (k) + K \cdot \varphi ^\prime (k) = L \cdot \varphi (k) = Q](Article/UploadFiles/200908/2009082109080061.png)
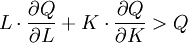 (9.14)
(9.14) 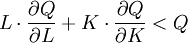 (9.15)
(9.15)