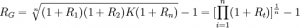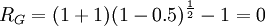几何平均收益率 发表评论(0) 编辑词条
什么是几何平均收益率
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1 + R1)元,第二期投资者会将(1 + R1)进行再投资,到第二期末价值则为(1 + R1)(1 + R2)元,……。
这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。
[编辑]几何平均收益率的公式
几何平均收益率(RG)的计算公式为:什么是几何平均收益率
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1 + R1)元,第二期投资者会将(1 + R1)进行再投资,到第二期末价值则为(1 + R1)(1 + R2)元,……。
这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。
[编辑]几何平均收益率的公式
几何平均收益率(RG)的计算公式为:
几何平均收益率的计算有个假定,即投资期间所获得的所有现金收益(如以现金形式派发的股息或红利等)都用于再投资。另外,它在计算过程中采用了即1加上收益率或用1减去亏损率的方法,进行如此技术处理的目的是为了避免几何平均数的计算因负的收益率的出现而变得毫无意义。
[编辑]几何平均收益率的例子
例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%(R1=(200-100)/100=1=100%),第2年的投资收益率则为-50%(R2= (100-200)/200=-0.5=-50%)。
实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,。这个计算结果符合实际情况,即两年来平均收益率为零
几何平均收益率的计算有个假定,即投资期间所获得的所有现金收益(如以现金形式派发的股息或红利等)都用于再投资。另外,它在计算过程中采用了即1加上收益率或用1减去亏损率的方法,进行如此技术处理的目的是为了避免几何平均数的计算因负的收益率的出现而变得毫无意义。
[编辑]几何平均收益率的例子
例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%(R1=(200-100)/100=1=100%),第2年的投资收益率则为-50%(R2= (100-200)/200=-0.5=-50%)。
实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1 + R1)元,第二期投资者会将(1 + R1)进行再投资,到第二期末价值则为(1 + R1)(1 + R2)元,……。
这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。
[编辑]几何平均收益率的公式
几何平均收益率(RG)的计算公式为:什么是几何平均收益率
几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1 + R1)元,第二期投资者会将(1 + R1)进行再投资,到第二期末价值则为(1 + R1)(1 + R2)元,……。
这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。
[编辑]几何平均收益率的公式
几何平均收益率(RG)的计算公式为:
几何平均收益率的计算有个假定,即投资期间所获得的所有现金收益(如以现金形式派发的股息或红利等)都用于再投资。另外,它在计算过程中采用了即1加上收益率或用1减去亏损率的方法,进行如此技术处理的目的是为了避免几何平均数的计算因负的收益率的出现而变得毫无意义。
[编辑]几何平均收益率的例子
例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%(R1=(200-100)/100=1=100%),第2年的投资收益率则为-50%(R2= (100-200)/200=-0.5=-50%)。
实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,。这个计算结果符合实际情况,即两年来平均收益率为零
几何平均收益率的计算有个假定,即投资期间所获得的所有现金收益(如以现金形式派发的股息或红利等)都用于再投资。另外,它在计算过程中采用了即1加上收益率或用1减去亏损率的方法,进行如此技术处理的目的是为了避免几何平均数的计算因负的收益率的出现而变得毫无意义。
[编辑]几何平均收益率的例子
例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%(R1=(200-100)/100=1=100%),第2年的投资收益率则为-50%(R2= (100-200)/200=-0.5=-50%)。
实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,
这个计算结果符合实际情况,即两年来平均收益率为零
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 几何平均收益率
收藏到: 

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条