不定积分 发表评论(0) 编辑词条

不定积分　　

　　设F(x)是函数f(x)的一个原函数，我们把函数f(x)的所有原函数F(x)+C（C为任意常数）叫做函数f(x)的不定积分。
　　记作∫f(x)dx。
　　其中∫叫做积分号，f(x)叫做被积函数，x叫做积分变量，f(x)dx叫做被积式，C叫做积分常数，求已知函数的不定积分的过程叫做对这个函数进行积分。
　　由定义可知：
　　求函数f(x)的不定积分，就是要求出f(x)的所有的原函数，由原函数的性质可知，只要求出函数f(x)的一个原函数，再加上任意的常数C，就得到函数f(x)的不定积分。
　　也可以表述成,积分是微分的逆运算,即知道了导函数,求原函数.

　　由不定积分定义，若F'(x)=f(x)，则∫f(x)dx=F(x)+C
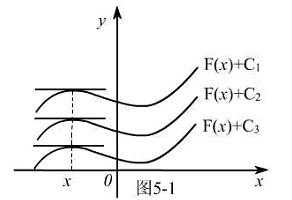
　　不定积分几何意义　F(x)+C为无穷多条曲线，通常称为f(x)的积分曲线族。由[F(x)+C]'=F'(x)=f(x)可知，在点x处，积分曲线族中每条曲线有相同的导数，按导数的几何意义，由相同的切线斜率，即切线平行，于是有：
　　∫f(x)dx表示一族曲线，族中每条曲线在点x处有平行的切线.
　　常见不定积分公式
　　1）∫0dx=c
　　2）∫x^udx=(x^u+1)/(u+1)+c
　　3）∫1/xdx=ln|x|+c
　　4)）∫a^xdx=(a^x)/lna+c
　　5）∫e^xdx=e^x+c
　　6）∫sinxdx=-cosx+c
　　7）∫cosxdx=sinx+c
　　8）∫1/(cosx)^2dx=tanx+c
　　9）∫1/(sinx)^2dx=-cotx+c
　　10）∫1/√（1-x^2)　dx=arcsinx+c
　　11）∫1/(1+x^2)dx=arctanx+c
　　12）∫1/(a^2-x^2)dx=(1/2a)ln|(a+x)/(a-x)|+c
　　13）∫secxdx=ln|secx+tanx|+c
　　14）∫1/(a^2+x^2)dx=1/a*arctan(x/a)+c
　　15）∫1/√(a^2-x^2)　dx=arcsin(x/a)+c
　　16) ∫sec^2 x dx=tanx+c;
　　17) ∫shx dx=chx+c;
　　18) ∫chx dx=shx+c;
　　19) ∫thx dx=ln(chx)+c;