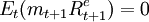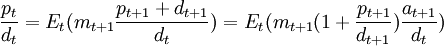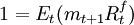随机贴现因子 发表评论(0) 编辑词条

随机贴现因子（stochastic discount factor，简称SDF）

　　随机贴现因子理论是最一般、最广泛适用的理论，无套利定价理论和风险中性定价理论均可以由随机贴现因子理论推导出来。

　　基于消费的跨期资本资产定价模型（ICAPM)。Merton（1973）。

　　Campbell（2000）通过随机贴现因子对资产定价问题进行了分析和回顾。

　　Cochrane（2000）将所有的资产定价问题纳入到随机贴现因子的一般框架之中，建立了一个比较完整的随机贴现因子理论体系。

　　如果一个贴现因子，能够满足：

　　p=E(mx)

　　或者用条件期望的形式：

　　p_t = E_t(m_{t + 1}x_{t + 1})

　　则我们称m或m_{t + 1}为随机贴现因子

　　提出的基本原则：基于消费的效用最大化

• 基于消费的资产定价模型认为，代表性投资者的效用来自于消费，其目标是终生效用最大化。为了实现其目标函数，投资者必须将财富在消费和投资之间进行分配。消费是为了满足现在的效用，而投资则是为了满足未来效用的需要。

• 目标函数：

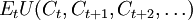
• 约束条件：

　　W_{t + 1} = (W_t − C_t)R_{t + 1} + e_{t + 1}

　　收益率：E_t(m_{t + 1}R_{t + 1}) = 1

　　超额收益率：

　　股票：

　　无风险资产：

　　欧式看涨期权：p_t = E_t(m_T(S_t − K) ⁺ )

　　定义：如果未来收益相同的资产具有相同的价格，则我们称一价定律成立。

　　定理1：一价定律等价于资产组合的价格是资产价格的线性组合。

　　定理2： 如果存在一个随机贴现因子，则一价定律成立。

　　定理3： 如果一价定律成立，则市场上存在一个随机贴现因子能够对资产定价。

　　从随机贴现因子也可以十分简单地推出贝塔定价模型。

　　从随机贴现因子理论中，还可以十分容易地推导出均值方差有限前沿理论。

　　CAPM理论、APT模型等，都可以在上述分析的基础上通过进一步演化得到。因此，总的来说，随机贴现因子理论为资产定价提供了一个最一般、最通用的分析框架。

• 贴现因子