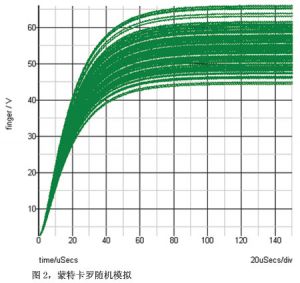
蒙特·卡罗方法 发表评论(0) 编辑词条

        

也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。蒙特·卡罗方法的名字来源于摩纳哥的一个城市蒙地卡羅，该城市以赌博业闻名，而蒙特·卡罗方法正是以概率为基础的方法。蒙特·卡罗方法在金融工程学，宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。

        当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。 有一个例子可以使你比较直观地了解蒙特卡罗方法：假设我们要计算一个不规则图形的面积，那么图形的不规则程度和分析性计算（比如，积分）的复杂程度是成正比的。蒙特卡罗方法是怎么计算的呢？假想你有一袋豆子，把豆子均匀地朝这个图形上撒，然后数这个图形之中有多少颗豆子，这个豆子的数目就是图形的面积。当你的豆子越小，撒的越多的时候，结果就越精确。在这里我们要假定豆子都在一个平面上，相互之间没有重叠。

       在解决实际问题的时候应用蒙特·卡罗方法主要有两部分工作：

1、用蒙特·卡罗方法模拟某一过程时，需要产生各种概率分布的随机变量。
2、用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。

    

   使用蒙特·卡罗方法进行分子模拟计算是按照以下步骤进行的：

1、使用随机数发生器产生一个随机的分子构型。
2、对此分子构型的其中粒子坐标做无规则的改变，产生一个新的分子构型。
3、计算新的分子构型的能量。
4、比较新的分子构型于改变前的分子构型的能量变化，判断是否接受该构型。
    若新的分子构型能量低于原分子构型的能量，则接受新的构型，使用这个构型重复再做下一次迭代。
    若新的分子构型能量高于原分子构型的能量，则計算玻尔兹曼因子，并产生一个随机数。
    若这个随机数大于所计算出的玻尔兹曼因子，则放弃这个构型，重新计算。
    若这个随机数小于所计算出的玻尔兹曼因子，则接受这个构型，使用这个构型重复再做下一次迭代。
5、如此进行迭代计算，直至最后搜索出低于所给能量条件的分子构型结束。

       

 通常蒙特·卡罗方法通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特·卡罗方法是一种有效的求出数值解的方法。一般蒙特·卡罗方法在数学中最常见的应用就是蒙特·卡罗积分。

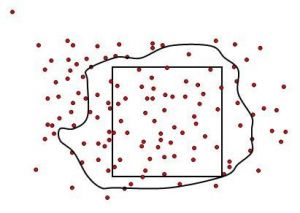
        非权重蒙特卡罗积分，也称确定性抽样，是对被积函数变量区间进行随机均匀抽样，然后对被抽样点的函数值求平均，从而可以得到函数积分的近似值。此种方法的正确性是基于概率论的中心极限定理。当抽样点数为m时，使用此种方法所得近似解的统计误差恒为,不随积分维数的改变而改变。因此当积分维度较高时，蒙特卡罗方法相对于其他数值解法更优。

1、http://zh.wikipedia.org/wiki/%E8%92%99%E7%89%B9%C2%B7%E5%8D%A1%E7%BD%97%E6%96%B9%E6%B3%95

2、http://wenda.tianya.cn/wenda/thread?tid=12934b419bf1cc84

3、http://so.pinggu.org/search.php?searchid=1042&orderby=lastpost&ascdesc=desc&searchsubmit=yes