投资函数 发表评论(0) 编辑词条
投资函数(Investment Function)
投资函数概述编辑本段回目录
投资函数模型编辑本段回目录
一、加速模型编辑本段回目录
- ⒈ 常见4类模型形式
It = f(ΔYt) + μt
It = f(Yt,Kt − 1) + μt
It = f(Yt,Yt − 1,It − 1) + μ
It = f(ΔYt,Yt − 1,It − 1) + μ
分别为后面4类加速模型。
- ⒉ 原始加速模型(Na?ve Accelerator Model)
1917年Clark提出
Ke = αY
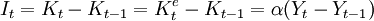
It = αΔYt + μ
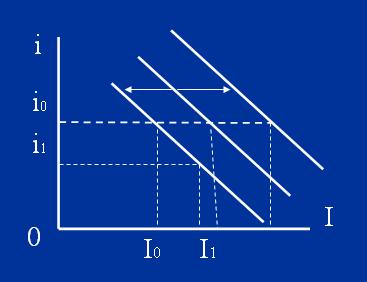
- ⒊ 灵活的加速模型(Flexible Accelerator Model)
Koyck于1954年
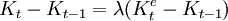
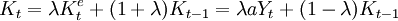
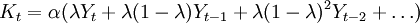
如果考虑到折旧,则有:
It = Kt − Kt − 1 + δKt − 1 = αλYt + (δ − λ)Kt − 1
It = αλYt + (δ − λ)Kt − 1 + μ
- ⒋ 实用的加速模型
利用It − 1 = Kt − 1 + (1 − δ)Kt − 2
It − (1 − δ)It − 1 = αλYt + (δ − λ)Kt − 1 − (1 − δ)αλYt − 1 − (1 − δ)(δ − λ)Kt − 2
= αλYt − (1 − δ)αλYt − 1 + (δ − λ)It − 1
It = αλYt − (1 − δ)αλYt − 1 + (1 − λ)It − 1 + μ
- ⒌ 利用最新信息的加速模型
Hines和Catephores于1970年指出,人们是根据产出水平的最新信息来确定资本存量的期望值,而不是根据尚未可知的实际产出水平。于是有
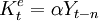
It = αλYt − n − (1 − δ)αλYt − n − 1 + (1 − λ)It − 1
= αλΔYt − n + δαλYt − n − 1 + (1 − λ)It − 1
It = αλΔYt − n + δαλYt − n − 1 + (1 − λ)It − 1 + μ
⒍ 对加速模型的评价
假设
- 没有资本闲置
- 资本产出比为常数
- 不存在自发投资
- 采用几何滞后
- 揭示了投资活动的原动力
- 从总体上反映了投资活动中的因果关系
- 具有较大的实际应用价值
二、利润决定的投资函数模型编辑本段回目录
- 1、假设
加速模型认为投资的原动力是产出的增长。
但由于投资活动是一个多周期过程,投资决策必然与资金的回报有关,所以就要考虑市场条件、税率、利率、产品与资本品的价格等因素。
所以,资本存量的预期值并不取决于产出水平,而是取决于利润水平。
- 2、模型
Grunfeld于1961年提出了资本存量的预期值与利润水平之间的关系:
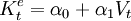
考虑资本存量的调整过程,投资函数模型为:
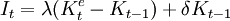
= λα0 + λα1Vt + (δ − λ)Kt − 1
其计量形态为:
It = λα0 + λα1Vt + (δ − λ)Kt − 1 + μ
先验地得到折旧率δ,然后估计模型的其它参数。
三、新古典投资函数模型编辑本段回目录
- 1、假设
加速模型假设资本产出比为常数,即认为资本与其它要素之间不具有可替代性。
戴尔·乔根森(Dale W. Jorgenson)将新古典生产函数引入投资函数模型,承认在生产函数中要素之间具有可替代性,提出了新古典投资函数模型。
- 2、模型
以利润最大为目标,以新古典生产函数为约束条件,求解如下极值问题:
MzxRt = ptYt − wtLt − wtLt − rtKt
约束:Yt = f(Kt,Lt)
其中R、p、w、r分别为利润、产品的价格、工资率和资本的租金。
求解该极值问题即得到资本的最优存量,以此决定投资。
该模型的求解过程利用了边际生产力条件,不适用。
四、一个中国的投资函数模型编辑本段回目录
- ⒈ 模型形式
常用的模型形式
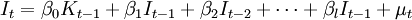
合理的经济解释
估计中的问题
- ⒉ 推导过程
根据经济行为,有
It = f1(Yt)
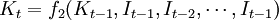
Yt = f3(Kt,Lt)
逐一代入,则得到上面所表示的投资函数模型 。
分别采用简单的线性关系表示上述3个函数,有
It = αtYt
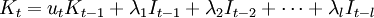
Yt = etKt
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 投资函数 Dale W. Jorgenson 产品 价格 信息 利润 利率 固定资产 国民收入 工资率 戴尔·乔根森

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条