函数 发表评论(0) 编辑词条
简介编辑本段回目录
函数定义:设A、B是两个集合,如果按照某种对应法则f,对于集合A中任何一个元素,在集合B中都有惟一的元素和它对应,这样的对应叫做从集合A到集合B的映射,记作f : A-->B. 当集合A,B都是非空的数的集合,且B的每一个元素都有原象时,这样的映射f:A-->B.就叫定义域A到值域B上的函数.
函数
在数学领域,函数是一种关系,这种关系使一个集合里的每一个元素对应到另一个(可能相同的)集合里的唯一元素。
----A variable so related to another that for each value assumed by one there is a value determined for the other.
应变量,函数一个与他量有关联的变量,这一量中的任何一值都能在他量中找到对应的固定值。
----A rule of correspondence between two sets such that there is a unique element in the second set assigned to each element in the first set.
函数两组元素一一对应的规则,第一组中的每个元素在第二组中只有唯一的对应量。
函数的概念对于数学和数量学的每一个分支来说都是最基础的。
术语函数,映射,对应,变换通常都有同一个意思。
但函数只表示数与数之间的对应关系,映射还可表示点与点之间,图形之间等的对应关系。可以说函数是一种特殊的映射。
历史 编辑本段回目录
笛卡儿引入变量后,随之而来的便是函数的概念.他指出y和是变量(“未知量和未定的量”)的时候,也注意到y依赖于而变.这正是函数思想的萌芽.但是他没有使用“函数”这个词.
函数这个数学名词是莱布尼兹在1694年开始使用的,以描述曲线的一个相关量,如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数,数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数。此两者描述了函数输出值的变化同输入值变化的关系,是微积分学的基础。
1718年,约翰·贝努里(en:Johann Bernoulli)把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”f(x) = sin(x) + x3
18世纪,欧拉曾经前后给出函数的三种定义:
1.将函数定义为“解析表示式”他写道:“变量的函数是一个解析表达式,它是由这个变量和一些常量以任何方式组成的.”
2.将函数定义为“由曲线确定的关系”:“在平面上徒手画出来的曲线所表示的y与之间的关系.”
3.将函数定义为“变量之间的依赖变化”.他说:“如果某些变量,以这样一种方式依赖于另一些变量,即当后面这些变量变化时,前面这些变量也随之而变化,则前面的变量称为后面变量的函数.”
用现代的眼光去看,这三种定义都有一定的局限性.第1种、第3种两种定义容易理解,所以现在仍然被一些通俗的读物所采用,缺点在于过分狭窄,因为许多函数是没有解析表达式的,也有些函数并不随自变量的变化而变化.第2个定义意义不够明确且局限于表达方式.不管怎样,欧拉定义对后世的影响很大.
1837年,德国数学家秋里赫勒进一步给出函数的定义:“对于在某区间上的每一个确定的值,y都有一个或多个确定的值,那么y叫做的函数.”这已经相当接近现在许多教科书所采用的定义.
1775年,欧拉在《微分学原理》一书中又提出了函数的一个定义:“如果某些量以如下方式依赖于另一些量,即当后者变化时,前者本身也发生变化,则称前一些量是后一些量的函数。”
19世纪的数学家开始对数学的各个分支作规范整理。维尔斯特拉斯(Karl Weierstrass)提出将微积分学建立在算术,而不是几何的基础上,因而更趋向于欧拉的定义。
通过扩展函数的定义,数学家能够对一些“奇怪”的数学对象进行研究,例如不可导的连续函数。这些函数曾经被认为只具有理论价值,迟至20世纪初时它们仍被视作“怪物”。稍后,人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。
到19世纪末,数学家开始尝试利用集合论来规范数学。他们试图将每一类数学对象定义为一个集合。狄利克雷(Johann Peter Gustav Lejeune Dirichlet)给出了现代正式的函数定义。狄利克雷的定义将函数视作数学关系的特例。然而对于实际应用的情况,现代定义和欧拉定义的区别可以忽略不计
19世纪70年代,康托的集合论出现之后,函数便明确地定义为集合间的对应关系.这是目前一般教科书所用的“集合对应”定义.
采用“集合对应”定义以后,摆脱了“变量”一词.
“变量”一词的意义至今尚不清楚.“自变量”这个提法本身也是有缺点的,因为变量必定依赖于时间而变,也就是它必定是时间的函数,不可能脱离时间而“自变量”.对于函数采用了“集合对应”定义以后,摆脱了“变量”与“自变量”等名词,定义函数无需再依赖于时间了.而变量这个词.许多学者主张废弃不用,有人主张将“自变量”“因变量”改为“第一值”“第二值”.
我国“函数”一词,是《代微积拾级》中首先使用的,这本书把函数定义为:“凡此变数中含彼变数,则此为彼之函数.”这里“函”是包含的意思.这定义大致相当于欧拉的解析表达式定义,在一个式子中“包含”着变量,那么这个式子就是的函数.
函数这个概念已成为数学中最重要的几个概念之一,而变量这个词却逐渐被新的词所代替.
通过扩展函数的定义,数学家能够对一些“奇怪”的数学对象进行研究,例如不可导的连续函数。这些函数曾经被认为只具有理论价值,迟至20世纪初时它们仍被视作“怪物”。稍后,人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。
到19世纪末,数学家开始尝试利用集合论来规范数学。他们试图将每一类数学对象定义为一个集合。狄利克雷(Johann Peter Gustav Lejeune Dirichlet)给出了现代正式的函数定义。狄利克雷的定义将函数视作数学关系的特例。然而对于实际应用的情况,现代定义和欧拉定义的区别可以忽略不计。
正式定义 编辑本段回目录
从输入值集合X到可能的输出值集合Y的函数f(记作 )是X与Y的关系,满足如下条件:
f是完全的:对集合X中任一元素X都有集合Y中的元素y满足xfy(x与y是f相关的)。即,对每一个输入值,y中都有且只有一个与之对应的输出值。
f是多对一的:若xfy且xfz,则y = z。即,多个输入可以映射到一个输出,但一个输入不能映射到多个输出。
定义域中任一x在对映域中唯一对应的y记为f(x)。
比上面定义更简明的表述如下:从X映射到Y的函数f是X与Y的直积X / timesY的子集。X中任一x都与Y中的y唯一对应,且有序对(x,y)属于f。
X与Y的关系若满足条件(1),则为多值函数。函数都是多值函数,但多值函数不都是函数。X与Y的关系若满足条件(2),则为偏函数。函数都是偏函数,但偏函数不都是函数。除非特别指明,本百科全书中的“函数”总是指同时满足以上两个条件的关系。 考虑如下例子:
完全,但非多对一。X中的元素3与Y中的两个元素b 和c 相关。因此这是多值函数,而不是函数。
多对一,但非完全。 X 的元素1未与Y 的任一元素相关。因此这是偏函数,而不是函数。
完全且多对一。因此这是从X到Y的函数。此函数可以表示为f ={(1, d), (2, d), (3, c)},或 F={d,if x=1;d, if x=2;d, if x=3
定义域、对映域和值域 编辑本段回目录
输入值的集合X被称为f 的定义域;可能的输出值的集合Y被称为f 的陪域。函数的值域是指定义域中全部元素通过映射f 得到的实际输出值的集合。注意,把对映域称作值域是不正确的,函数的值域是函数的对映域的子集。
计算机科学中,参数和返回值的数据类型分别确定了子程序的定义域和对映域。因此定义域和对映域是函数一开始就确定的强制约束。另一方面,值域和实际的实现有关。
单射、满射与双射函数 编辑本段回目录
单射函数,将不同的变量映射到不同的值。即:若x和y属于定义域,则仅当x = y时有f(x) = f(y)。
满射函数,其值域即为其对映域。即:对映射f的对映域中之任意y,都存在至少一个x满足f(x) = y。
双射函数,既是单射的又是满射的。也叫一一对应。双射函数经常被用于表明集合X和Y是等势的,即有一样的基数。如果在两个集合之间可以建立一个一一对应,则说这两个集合等势。
像和原象 编辑本段回目录
元素 x∈X在 f 的像 就是 f(x)。
子集 A⊂X 在 f 的像是以其元素的像组成 Y的子集,即
f(A) := {f(x) : x ∈ A}。
注意 f 的值域就是定义域 X 的像 f(X)。在我们的例子里, {2,3} 在 f 的像是 f({2, 3}) = {c, d} 而 f 的值域是 {c, d}。
根据此定义,f 可引申成为由 X 的幂集(由 X 的子集组成的集)到 Y 的幂集之函数,亦记作 f。
子集 B ⊂ Y 在 f 的原像(或逆像)是如下定义 X的子集:
f −1(B) := {x ∈ X : f(x)∈B}。
在我们的例子里,{a, b} 的原像是 f −1({a, b}) = {1}。
根据此定义,f −1 是由 Y 的幂集到 X 的幂集之函数。
以下是 f 及 f −1 的一些特性:
f(A1 ∪ A2) = f(A1) ∪ f(A2).
f(A1 ∩ A2) ⊆ f(A1) ∩ f(A2).
f −1(B1 ∪ B2) = f −1(B1) ∪ f −1(B2).
f −1(B1 ∩ B2) = f −1(B1) ∩ f −1(B2).
f(f −1(B)) ⊆ B.
f −1(f(A)) ⊇ A.
这些特性适合定义域的任意子集 A, A1 及 A2 和输出值域的任意子集 B, B1 及 B2,甚至可推广到任意子集群的交集和并集。
函数图像 编辑本段回目录
立方函数的图像函数f 的图像是平面上点对(x,f(x))的集合,其中x取定义域上所有成员的。函数图像可以帮助理解证明一些定理。
如果X 和Y 都是连续的线,则函数的图像有很直观表示,如右图是立方函数的图像:
注意两个集合X 和Y 的二元关系有两个定义:一是三元组(X,Y,G),其中G 是关系的图;二是索性以关系的图定义。用第二个定义则函数 f 等于其图象。
函数范例 编辑本段回目录
首都之于国家(若不把多首都国[1]计算在内)。
每个自然数 n 的平方 n² 是n 的函数。
对数函数。 ln x 是正实数 x 的函数。注意,在 x 为负实数时没有定义 ln x。
对每个在 平面上的点,其和原点 (0, 0) 的距离是确定的。
常用的数学函数包括多项式函数、根式函数、幂函数、对数函数、有理函数、三角函数、反三角函数等。它们都是初等函数。非初等函数(或特殊函数)包括 伽傌函数和Bessel函数等。
函数的特性 编辑本段回目录
函数的单调性
1、A为函数f(x)定义域内某一区间, 任意取x1,x2,且x1<x2,比较f(x1),f(x2)的大小
2、单调性的判定:作差f(x1)-f(x2)判定;根据函数图象判定;
3、复合函数的单调性的判定:f(x),g(x) 同增、同减,f(g(x)) 为增函数,f(x),g(x)一增、一减,f(g(x)) 为减函数。
函数的奇偶性
1、 函数f(x)的定义域为D,x∈D ,f(-x)=f(x) → f(x)是偶函数;f(-x)=-f(x)→是奇函数。
2、 奇偶性的判定:作和差f(-x)± f(x)=0 判定;作商f(x)/f(-x)= ±1,f(x)≠0 判定
3、 奇、偶函数的必要条件是:函数的定义域关于原点对称;
4、 函数的图象关于原点对称 奇函数;
函数的图象关y轴对称 偶函数
5、 函数既为奇函数又为偶函数 f(x)=0,且定义域关于原点对称;
6、 复合函数的奇偶性:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇。
函数的周期性
1、设函数y=f(x)的定义域为D,x∈D,存在非0常数T,有f(x+T)=f(x) →
f(x)为周期函数,T为f(x)的一个周期;
2、 正弦、余弦函数的最小正周期为2π,函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期是T = 2π/|ω| ;
3、 正切、余切函数的最小正周期为π,函数y=Atan(ωx+φ)和y=Acot(ωx+φ)的周期是T=π/|ω| ;
4、 周期的求法:定义域法;公式法;最小公倍数法;利用函数的图象法;
5、 一般地,sinωx 和cosωx类函数加绝对值或平方后周期减半,tanωx 和cotωx类函数加绝对值或平方后周期不变。如:y=|cos2x| 的周期是π/2 ,y=|cotx|的周期是π。
函数分类 编辑本段回目录
函数可分为
奇函数或偶函数
连续函数或不连续函数
实函数或虚函数
标量函数或向量函数
歧义函数 编辑本段回目录
歧义函数指可于一条数学等式中找到不少于一个正确答案。例如,4的平方根可以是2或者-2而两者的平方皆是4。
严格来说,歧义函数不完全算是函数,因为数学函数的定义对于一个输入值只能有唯一一个输出值。实际上,这样的“函数”通常被称为关系式。
大陆的名称叫多值函数
n-元函数: 多元函数 编辑本段回目录
n-元函数是指输入值为 n-元组的函数。或者说,若一函数的输入值域为 n 个集合的积集的子集,这函数就是 n-元函数。例如, 距离函数 dist((x,y)) 是一个二元函数,输入值是由两个点组成的序对。另外,多复变函数(即输入值为复数的多元组)是一个重要的数学课题。
在抽象代数中, 算子其实都是函数,如乘法 "*" 是个二元函数:我们写 x*y 其实是 *(x,y)的中缀表达法。
函数式程序设计是一个以函数概念为中心的重要理论范例,其中的运算对象为多元函数,基本语法基于λ演算,而函数的复合(见下)则采用代换来完成。特别地,通过一种称为Currying的变换,可将多元函数变换为一元函数。
三角函数 编辑本段回目录
三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
由于三角函数的周期性,它并不具有单值函数意义上的反函数。
三角函数在复数中有较为重要的应用。在物理学中,三角函数也是常用的工具。
它有六种基本函数:
函数名 正弦 余弦 正切 余切 正割 余割
符号 sin cos tan cot sec csc
正弦函数 sin(A)=a/h
余弦函数 cos(A)=b/h
正切函数 tan(A)=a/b
余切函数 cot(A)=b/a
在某一变化过程中,两个变量x、y,对于某一范围内的x的每一个值,y都有确定的值和它对应,y就是x的函数。这种关系一般用y=f(x)来表示。
二次函数 编辑本段回目录
I.定义与定义表达式
一般地,自变量x和因变量y之间存在如下关系:
y=ax²+bx+c(a,b,c为常数,a≠0)
则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
II.二次函数的三种表达式
一般式:y=ax²+bx+c(a,b,c为常数,a≠0)
顶点式:y=a(x-h)²+k [抛物线的顶点P(h,k)]
交点式:y=a(x-x1)(x-x2) [仅限于与x轴有交点A(x1,0)和 B(x2,0)的抛物线]
注:在3种形式的互相转化中,有如下关系:
h=-b/2a k=(4ac-b²)/4a x1,x2=(-b±√b²-4ac)/2a
III.二次函数的图象
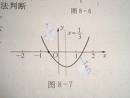
在平面直角坐标系中作出二次函数y=x²的图象,
可以看出,二次函数的图象是一条抛物线。
IV.抛物线的性质
1.抛物线是轴对称图形。对称轴为直线
x = -b/2a。
对称轴与抛物线唯一的交点为抛物线的顶点P。
特别地,当b=0时,抛物线的对称轴是y轴(即直线x=0)
2.抛物线有一个顶点P,坐标为
P [ -b/2a ,(4ac-b²)/4a ]。
当-b/2a=0时,P在y轴上;当Δ= b²-4ac=0时,P在x轴上。
3.二次项系数a决定抛物线的开口方向和大小。
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
|a|越大,则抛物线的开口越小。
4.一次项系数b和二次项系数a共同决定对称轴的位置。
当a与b同号时(即ab>0),对称轴在y轴左;
当a与b异号时(即ab<0),对称轴在y轴右。
5.常数项c决定抛物线与y轴交点。
抛物线与y轴交于(0,c)
6.抛物线与x轴交点个数
Δ= b²-4ac>0时,抛物线与x轴有2个交点。
Δ= b²-4ac=0时,抛物线与x轴有1个交点。
Δ= b²-4ac<0时,抛物线与x轴没有交点。
V.二次函数与一元二次方程
特别地,二次函数(以下称函数)y=ax²+bx+c,
当y=0时,二次函数为关于x的一元二次方程(以下称方程),
即ax²+bx+c=0
此时,函数图象与x轴有无交点即方程有无实数根。
函数与x轴交点的横坐标即为方程的根。
一次函数 编辑本段回目录
I、定义与定义式:
自变量x和因变量y有如下关系:
y=kx+b(k,b为常数,k≠0)
则称y是x的一次函数。
特别地,当b=0时,y是x的正比例函数。
II、一次函数的性质:
y的变化值与对应的x的变化值成正比例,比值为k
即 △y/△x=k
III、一次函数的图象及性质:
1. 作法与图形:通过如下3个步骤(1)列表;(2)描点;(3)连线,可以作出一次函数的图象——一条直线。因此,作一次函数的图象只需知道2点,并连成直线即可。
2. 性质:在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
3. k,b与函数图象所在象限。
当k>0时,直线必通过一、三象限,y随x的增大而增大;
当k<0时,直线必通过二、四象限,y随x的增大而减小。
当b>0时,直线必通过一、二象限;当b<0时,直线必通过三、四象限。
特别地,当b=O时,直线通过原点O(0,0)表示的是正比例函数的图象。
这时,当k>0时,直线只通过一、三象限;当k<0时,直线只通过二、四象限。
IV、确定一次函数的表达式:
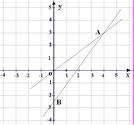
已知点A(x1,y1);B(x2,y2),请确定过点A、B的一次函数的表达式。
(1)设一次函数的表达式(也叫解析式)为y=kx+b。
(2)因为在一次函数上的任意一点P(x,y),都满足等式y=kx+b。所以可以列出2个方程:
y1=kx1+b① 和 y2=kx2+b②。
(3)解这个二元一次方程,得到k,b的值。
(4)最后得到一次函数的表达式。
V、一次函数在生活中的应用
1.当时间t一定,距离s是速度v的一次函数。s=vt。
2.当水池抽水速度f一定,水池中水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
反比例函数 编辑本段回目录
形如 y=k/x(k为常数且k≠0) 的函数,叫做反比例函数。
自变量x的取值范围是不等于0的一切实数。
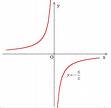
反比例函数的图像为双曲线。
如图,上面给出了k分别为正和负(2和-2)时的函数图像。
三角函数
三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
由于三角函数的周期性,它并不具有单值函数意义上的反函数。
三角函数在复数中有较为重要的应用。在物理学中,三角函数也是常用的工具。
在数学领域,函数是一种关系,这种关系使一个集合里的每一个元素对应到另一个(可能相同的)集合里的唯一元素。函数的概念对于数学和数量学的每一个分支来说都是最基础的。
术语函数,映射,对应,变换通常都是同一个意思。
简而言之,函数是将唯一的输出值赋予每一输入的“法则”。这一“法则”可以用函数表达式、数学关系,或者一个将输入值与输出值对应列出的简单表格来表示。函数最重要的性质是其决定性,即同一输入总是对应同一输出(注意,反之未必成立)。从这种视角,可以将函数看作“机器”或者“黑盒”,它将有效的输入值变换为唯一的输出值。通常将输入值称作函数的参数,将输出值称作函数的值。
最常见的函数的参数和函数值都是数,其对应关系用函数式表示,函数值可以通过直接将参数值代入函数式得到。如下例,
f(x) = x2 ,x 的平方即是函数值。
也可以将函数很简单的推广到与多个参量相关的情况。例如:
g(x,y) = xy 有两个参量x和y,以乘积xy为值。与前面不同,这一“法则”与两个输入相关。其实,可以将这两个输入看作一个有序对(x, y),记g为以这个有序对(x, y)作参数的函数,这个函数的值是xy。
科学研究中经常出现未知或不能给出表达式的函数。例如地球上不同时刻温度的分布,这一函数以地点和时间为参量,以某一地点、某一时刻的温度作为输出。
函数的概念并不局限于数的计算,甚至也不局限于计算。函数的数学概念更为宽泛,而且不仅仅包括数之间的映射关系。函数将“定义域”(输入集)与“对映域”(可能输出集)联系起来,使得定义域的每一个元素都唯一对应对映域中的一个元素。函数,如下文所述,被抽象定义为确定的数学关系。由于函数定义的一般性,函数概念对于几乎所有的数学分支都是很基本的。
复合函数 编辑本段回目录
有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数:
x→u→y,这要看定义域:设ψ的定义域为U 。 f的值域为U,当U*ÍU时,称f与ψ 构成一个复合函数 , 例如 y=lgsinx,x∈(0,π)。此时sinx>0 ,lgsinx有意义 。但如若规定x∈(-π,0),此时sinx<0 ,lgsinx无意义 ,就成不了复合函数。
反函数 编辑本段回目录
就关系而言,一般是双向的 ,函数也如此 ,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程 ,即x成了y的函数 ,记 为x=f -1(y)。称f -1为f的反函数。习惯上用x表示自变量 ,故这个函数仍记为y=f -1(x) ,例如 y=sinx与y=arcsinx 互为反函数。在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。
隐函数 编辑本段回目录
若能由函数方程 F(x,y)=0 确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。
多元函数 编辑本段回目录
设点(x1,x2,…,xn) ∈GÍRn,UÍR1 ,若对每一点(x1,x2,…,xn)∈G,由某规则f有唯一的 u∈U与之对应:f:G→U,u=f(x1,x2,…,xn),则称f为一个n元函数,G为定义域,U为值域。
基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。
①幂函数:y=xμ(μ≠0,μ为任意实数)定义域:μ为正整数时为(-∞,+∞),μ为负整数时是(-∞,0)∪(0,+∞);μ=(α为整数),当α是奇数时为( -∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为的复合函数进行讨论。略图如图2、图3。
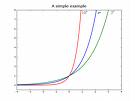
②指数函数:y=ax(a>0 ,a≠1),定义成为( -∞,+∞),值域为(0 ,+∞),a>0 时是严格单调增加的函数( 即当x2>x1时,) ,0<a<1 时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=()x的图形关于y轴对称。如图4。
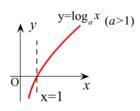
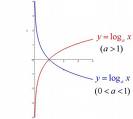
③对数函数:y=logax(a>0), 称a为底 , 定义域为(0,+∞),值域为(-∞,+∞) 。a>1 时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数 。如图5。
以10为底的对数称为常用对数 ,简记为lgx 。在科学技术中普遍使用的是以e为底的对数,即自然对数,记作lnx。
④三角函数。
正弦函数、余弦函数。
⑤反三角函数:双曲正、余弦
⑥双曲函数:双曲正弦(ex-e-x),双曲余弦?(ex+e-x),双曲正切(ex-e-x)/(ex+e-x) ,双曲余切( ex+e-x)/(ex-e-x)。
在数学领域,函数是一种关系,这种关系使一个集合里的每一个元素对应到另一个(可能相同的)集合里的唯一元素(这只是一元函数f(x)=y的情况,请按英文原文把普遍定义给出,谢谢)。函数的概念对于数学和数量学的每一个分支来说都是最基础的。
术语函数,映射,对应,变换通常都是同一个意思。
幂函数 编辑本段回目录
1、函数y=xa 叫做幂函数,其中x是自变量,指数a为常量,它可以是任意实数。
2、幂函数的性质:
由其定义域所出现的特征我们知道,幂函数y=xa的图像和性质与指数a有密切的关系,a>0时,
由上图可以看出这四个函数有下列性质:
(1)图像都通过原点和(1,1)点
(2)在区间(0,+ )内,曲线从左到右逐渐上升,即函数Y的值随X仁政的增大而增大,这时,我们称函数在区间(0,+ )内单调增加。
(3)Y=X和Y=X3 的图像关于坐档原点对称; Y=X2的图像关于Y轴对称, 的图像既不关于原点对称,也不关于Y轴对称。
总结:由以上特征可知当a>0时,幂函数y=xa 具有下列性质。
①图像都过原点和点(1,1)
②函数y在区间(0,+ )内的值随x值的增大而增大(单调递增)。
注:我们把图像关于原点对称的函数称为奇函数;图像关于Y轴以称的函数称为偶函数,图像既不关于原点对称,又不关于Y轴对称的函数称为非奇非偶函数。
2)当a<0时,幂函数情形
a<0
由图可以看出这三个函数有以下性质:
(1)图像都过点(1,1)
(2)在区间(0,+ )内,曲线从左到右逐渐下降,即函数值随X值的增大而减小,这时我们称函数在区间(0,+ )内单调减小。
(3) 的图像关于原点对称, 的图像关于Y轴对称, 的图像既不对称于原点,也不对称于Y轴。
总结:由以上特征可知当a<0时幂函数 具有下列性质。
① 图像都通过(1,1)点
② 函数在区间(0,+ )内的值随X值的增大而减小(单调递减)。
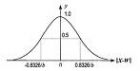
高斯函数编辑本段回目录
设x∈R , 用 [x]或int(x)表示不超过x 的最大整数,并用表示x的非负纯小数,则 y= [x] 称为高斯(Guass)函数,也叫取整函数。
任意一个实数都能写成整数与非负纯小数之和,即:x= [x] + (0≤<1)
函数关系 编辑本段回目录
函数关系是满足一定条件的一种关系。
现在用集合的语言给出函数关系的定义:
若D是一个非空实数集合,设有一个对应规则f,使每一个x∈D,都有一个确定的实数y与之对应,则称这个对应规则f为定义在D上的一个函数关系,或称变量y变量x的函数。记作y=f(x),x∈D。
X称为自变量,y称为因变量。
集合D称为函数的定义域,也可以记作D(f)。
对于x0∈D(f)所对应的y值,记作y0或f(x0)或y∣x=x0,称为当x=x0时函数y=f(x)的函数值。
全体函数值的集合{y∣y=f(x),x∈D(f)},称为函数y=f(x)的值域,记作Z或Z(f)。
函数f(x)中的f反映自变量与因变量的对应规则。对应规则也常常用φ,h,g,F等表示,那么函数也就记作φ(x),h(x),g(x),F(x)等。有时为简化符号,函数关系也可记作y=y(x),此时等号左边的y表示函数值,右边的y表示对应规则。
在平面直角坐标系中,取自变量在横轴上变化,因变量在纵轴上变化,则平面点集{(x,y)∣y=f(x),x∈D(f)}即为定义在D(f)上的函数y=f(x)的图形。
本词条由以下会员参与贡献
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条