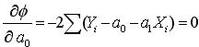OSL 发表评论(0) 编辑词条

普通最小二乘法（method of ordinary least squares）普通最小二乘法具有良好的统计性质。之所以称为普通最小二乘法，是因为还有一种方法称为广义最小二乘法，普通最小二乘法只是它的一个特例。

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

用各个离差的平方和M=Σ(i=1到n)[yi-(axi+b)]^2最小来保证每个离差的绝对值都很小。解方程组∂M/∂a=0；∂M/∂b=0，整理得(Σxi^2)a+(Σxi)b=Σxiyi；(Σxi)a+nb=Σyi。解出a,b。
　　在我们研究两个变量(x, y)之间的相互关系时，通常可以得到一系列成对的数据(x1, y1、x2, y2... xm , ym)；将这些数据描绘在x -y直角坐标系中, 若发现这些点在一条直线附近，可以令这条直线方程如(式1-1)。
　　Y计= a0 + a1 X (式1-1)
　　其中：a0、a1 是任意实数
　　为建立这直线方程就要确定a0和a1，应用《最小二乘法原理》，将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi - Y计)2〕最小为“优化判据”。
　　令: φ = ∑(Yi - Y计)2 (式1-2)
　　把(式1-1)代入(式1-2)中得:
　　φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)
　　当∑(Yi-Y计)平方最小时，可用函数 φ 对a0、a1求偏导数，令这两个偏导数等于零。
　　(式1-4)
　　(式1-5)
　　亦即：
　　m a0 + (∑Xi ) a1 = ∑Yi (式1-6)
　　(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi, Yi) (式1-7)
　　得到的两个关于a0、 a1为未知数的两个方程组，解这两个方程组得出：
　　a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)
　　a1 = [n∑Xi Yi - (∑Xi ∑Yi)] / [n∑Xi2 - (∑Xi)2 )] (式1-9)
　　这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即：数学模型。
　　在回归过程中，回归的关联式是不可能全部通过每个回归数据点(x1, y1、 x2, y2...xm,ym),为了判断关联式的好坏,可借助相关系数“R”，统计量“F”，剩余标准偏差“S”进行判断；“R”越趋近于 1 越好；“F”的绝对值越大越好；“S”越趋近于 0 越好。
　　R = [∑XiYi - m (∑Xi / m)(∑Yi / m)]/ SQR{[∑Xi2 - m (∑Xi / m)2][∑Yi2 - m (∑Yi / m)2]} (式1-10) ＊
　　在(式1-1)中，m为样本容量，即实验次数；Xi、Yi分别任意一组实验X、Y的数值。