平行四边形 发表评论(0) 编辑词条

　　在同一平面内两组对边分别平行的四边形叫做平行四边形(parallelogram)。

　　平行四边形对角相等，对边平行且相等，邻角互补（相加角度为180度）。矩形，菱形，正方形都是特殊的平行四边形。
定义
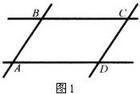
　　　（1）如果一个四边形是平行四边形，那么这个平行四边形的一组对边平行且相等。
　　（简述为“平行四边形的对边平行且相等”）
　　（2）如果一个四边形是平行四边形，那么这个平行四边形的两组对边分别平行。
　　（简述为“平行四边形的对边平行”）
　　（3）如果一个四边形是平行四边形，那么这个平行四边形的两组对边分别相等。
　　（简述为“平行四边形的对边相等”）
　　（4）如果一个四边形是平行四边形，那么这个平行四边形的两组对角分别相等。
　　（简述为“平行四边形的对角相等”）
　　（5）如果一个四边形是平行四边形，那么这个平行四边形的两条对角线互相平分。
　　（简述为“平行四边形的两条对角线互相平分”）
　　（6）平行四边形是中心对称图形，对称中心是两条对角线的交点。
　　（7）一般的平行四边形不是轴对称图形。

　　　（1）两组对边分别相等的四边形是平行四边形。
　　（2）对角线互相平分的四边形是平行四边形。
　　（3）一组对边平行且相等的四边形是平行四边形。
　　（4）两组对边分别平行的四边形是平行四边形。
　　（5）两组对角分别相等的四边形是平行四边形。（不可直接证明为平行四边形）

　　（1）连接任意四边形各边的中点所得图形是平行四边形。
　　（2）平行四边形的对角相等，两邻角互补。
　　（3）过平行四边形对角线交点的直线，将平行四边形分成全等的两部分图形。
　　（4）平行四边形是中心对称图形，对称中心是两对角线的交点。性质6
　　（5）平行四边形的面积等于底和高的积。（可视为矩形）
　　（6）平行四边形ABCD中（如图）E为AB的中点，则AC和DE互相三等分，
　　一般地，若E为AB上靠近A的n等分点，则AC和DE互相(n+1)等分。

　　一、连结对角线或平移对角线。
　　二、过顶点作对边的垂线构成直角三角形。
　　三、连结对角线交点与一边中点，或过对角线交点作一边的平行线，构成线段平行或中位线。
　　四、连结顶点与对边上一点的线段或延长这条线段，构造相似三角形或等积三角形。
　　五、过顶点作对角线的垂线，构成线段平行或三角形全等。

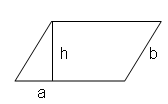
　　1、平行四边形的面积公式：底×高（推导方法如图）；如用“h”表示高，“a”表示底，“s”表示平行四边形面积，
　　则S平行四边=ah
　　2、平行四边形周长可以二乘（底1+底2）；如用“a”表示底1，“b”表示底2，“c平”表示平行四边形周长，
　　则平行四边的周长c=2(a+b)

　　1、平行四边形属于平面图形。
　　2、平行四边形属于四边形。
　　3、平行四边形中还包括特殊的平行四边形：长方形、正方形和菱形等。