防色狼公式 发表评论(0) 编辑词条

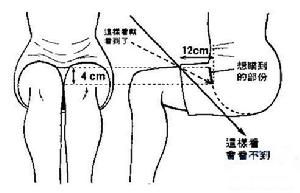
图1：假设女孩双膝并隆的点和裙子上缘距离4公分..

而裙摆到小裤裤之间的距离是12公分..

那么从侧面看来..

目标区域和裙子就会形成一个直角三角形abc

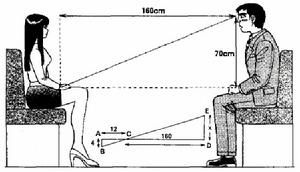
 图2：如果"观察者"的双眼e正好在bc线段的延长线上..　　

那么b点就会落在他的视野内.. 　　

如果我们做一条过e并垂直於ac线段延长线的直线de的话.

直角三角形dec就会和直角三角形abc相似.

在△abc中.. 　　
ab的长度是ac的三分之一.. 　　
因此在abc里.. 　
de的长度也应该是dc的三分之一.. 　
又因为dc是观察者的眼睛与裙子之间的水平距离.. 　　
假设这个距离是1.6公尺.. 　
那么de的长度(眼睛距离裙摆的高度)x就是53.3公分.. 　
不过一个身高170公分的观察者在采取普通坐姿时..　　
他的眼睛与裙摆之间却会有70公分的差距.. 　　
换句话说.. 　　
他必须要把头向下低个17公分.. 　　
而且为了达成这个目标.. 　
得要让屁股向前挺出45公分才行..

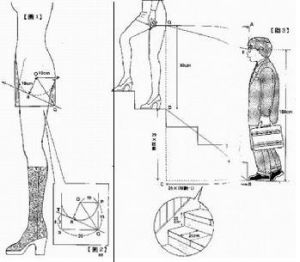
一般"观察者"想看的地方.. 　
其实是半径10公分的半球体部分.. 　
而裙子则与半球体相切并以向下15公分的剪裁.. 　
巧妙地遮住了观察者的视线.. 　
从上图看来. 　
直角三角形opq和orq是全等的. 　
如果将qr线段(也就是观察者视线)延长并做出另一个直角三角形tsq.. 　
那我们可由计算知道它的高是8.3公分..
tsq的高是底的0.415倍.. 所以.. 　
所以观察者如果想看到裙底风光.. 
最低限度是让视线的仰角大於角tqs.. 
也就是高和底的比值要大於0.415倍..