柯尼斯堡七桥问题 发表评论(0) 编辑词条

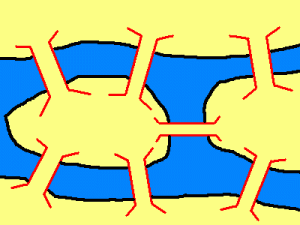
18世纪初在普鲁士柯尼斯堡镇（今苏联加里宁格勒）流传一个问题。这问题是城内一条河的两

支流绕过一个岛，有七座桥横跨这两支流。问一个散步者能否走过每一座桥，而每座桥却只走过一次。

柯尼斯堡七桥问题

柯尼斯堡七桥问题

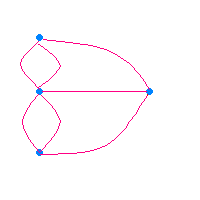
    欧拉在1736年圆满地解决了这一问题，证明这种方法并不存在。他在圣彼得堡科学院发表了图论史上第一篇重要文献。欧拉把实际的抽象问题简化为平面上的点与线组合，每一座桥视为一条线 ，桥所连接的地区视为点。这样若从某点出发后最后再回到这点，则这一点的线数必须是偶数。

    欧拉最后给出任意一种河──桥图能否全部走一次的判定法则。如果通奇数座桥的地方不止 两个，那么满足要求的路线便不存在了。如果只有两个地方通奇数座桥，则可从其中任何一地出发 找到所要求的路线。若没有一个地 方通奇数座桥，则从任何一地出发，所求的路线都能实现，他还 说明了怎样快速找到所要求的路线。  

    七桥问题引发了网络理论之研究，被认为是拓扑学理论基本应用题，对解决最短邮路等问 题很有帮助。