质量损失函数 发表评论(0) 编辑词条

1 成本相同的假定
       组装某种电源电路，需要一些原材料（如焊接材料等）、元器件。譬如需要某种型号的三级品的电阻。这种同一型号的三级品电阻，质量仍有好有坏。按质论价，价值应该不同。但通常买进的价格是一样的。利用这些原材料、元器件，加工成电源电路，每部的加工费（管理费、工资、能源的损耗、机器与厂房的磨损折旧、参观招待费等等）也不尽相同。因此，仔细追究起来，每部电源电路的成本是不全相同的。假若这个月组装了6000部电源电路，其材料费为233000元，加工费为7000元，则平均成本=40元/部
      每部电源电路的成本虽然不尽相同，但我们近似地假定它们的成本是相同的，是用了平均成本去作为每一部电源电路的成本。
      损失函数=质量损失函数+成本损失函数。既然成本被假定为相同，故总损失的大小取决于质量损失函数的高低。
2 质量损失函数及其近似表达式
      某种彩色电视机的电源电路，是要求把交流220伏的输入，变为直流100伏的输出。在成本相同的假定下，电源电路质量的好坏，除经久耐用之外，主要是要求直流输出能稳定在标准中心值100伏附近。越接近100伏，质量越好，所造成的损失越小；越离开100伏，质量越差，所造成的损失越大。
       一般地，随着产品指标值y（如上面的电源电路的直流输出电压）的变化，产品的质量所造成的损失q(y)也随着变化。
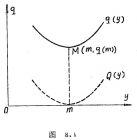
       在很多情况下，质量损失函数q(y)的曲线如图8.1那样，是中间低、两头高的。它在某一点M[m, q(m)]处最低（例如，上面电源电路中的m=100），即由质量造成的损失最小。y越偏离m，由质量造成的损失越大。

质量损失函数

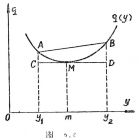
曲线q(y)在y=m的附近，曲线弧AB可以用割线AB代替，而割线的极限状态是曲线有点M处的切线CD。当y1、y2越接近m时，三种线（曲线、割线、切线）越相互靠近，用切线（一次式）来代替曲线的近似其近似程度就越好；当y1、y2离m稍远时，这种用切线来代替曲线的近似其近似程度就可能不好了。这时可以用通过三点A、M、B的二次曲线来近似代替（参看图8.2）。用二次曲线代替曲线q(y)比用切线代替的范围可以扩大一些，即可以离开点M更远一些。当然，如果离开点M太远，就是用二次曲线来代替，近似程度有时候也是不好的。

质量损失函数

下面用数学推导把这个现象再说明一遍。假定q(y)在y=m处存在二阶导数，则按泰勒公式有：

q(y)=q(m)+ q’(m)(y-m)/1!+ q’’(m)(y-m)2/2!+o[(y-m)2] (1)

由于q(y)在y=m处取极小值，所以有q’(m)=0. 故
q(y)=q(m)+ k(y-m)2 （2）
其中k=q’’(m)/21是不依赖于y的常数。即质量损失函数在y=m附近近似地等于一条抛物线（二次函数）。 令 Q(y)=q(y)-q(m)，

得 Q(y)=k(y-m)2 （3）

Q(y)和q(y)仅相差一个常数q(m)，不影响对于不同的y值，损失大小的相对比较。Q(y)也称作质量损失函数。今后，对于不同的y值，我们用Q(y)的近似表达式k(y-m)2来比较损失的大小。
当生产一件产品，其指标为y时，其相对的质量损失由Q(y)=k(y-m)2来计算。当产品不只一件时，我们记E[(y-m)2]=V，称V为偏差均方。每件产品的平均损失由Q=kV来计算。其中特别当E(y)=m时，则√V 为标准差。