根轨迹法发表评论(0) 编辑词条

　　在时域分析中已经看到，控制系统的性能取决于系统的闭环传递函数，因此，可以根据系统闭环传递函数的零、极点研究控制系统性能。但对于高阶系统，采用解析法求取系统的闭环特征方程根（闭环极点）通常是比较困难的，且当系统某一参数（如开环增益）发生变化时，又需要重新计算，这就给系统分析带来很大的不便。

　　1948年，伊万思根据反馈系统中开、闭环传递函数间的内在联系，提出了求解闭环特征方程根的比较简易的图解方法，这种方法称为根轨迹法。因为根轨迹法直观形象，所以在控制工程中获得了广泛应用。

　　根轨迹是当开环系统某一参数（如根轨迹增益）从零变化到无穷时，闭环特征方程的根在S平面上移动的轨迹。根轨迹增益 $K *$ 是首1形式开环传递函数对应的系数。

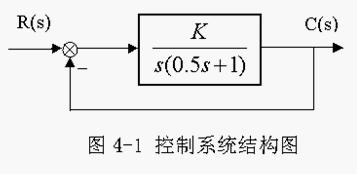
　　在介绍图解法之前，先用直接求根的方法来说明根轨迹的含义。控制系统如图4-1所示。其开环传递函数为:

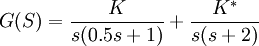
　　 $G(S)=\frac{K}{s(0.5s+1)}+\frac{K^*}{s(s+2)}$

　　根轨迹增益。闭环传递函数为:

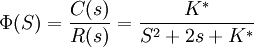
　　 $\Phi(S)=\frac{C(s)}{R(s)}=\frac{K^*}{S^2+2s+K^*}$

　　闭环特征方程为:

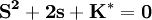
　　 $\mathbf{S^2+2s+K^*=0}$

　　特征根为：

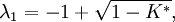
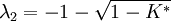
　　 $\lambda_1=-1+\sqrt{1-K^*} ,$ 　　 $\lambda_2=-1-\sqrt{1-K^*}$

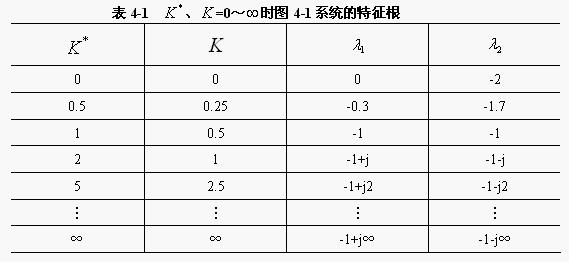
　　当系统参数K^*（或K）从零变化到无穷大时，闭环极点的变化情况见表4-1:

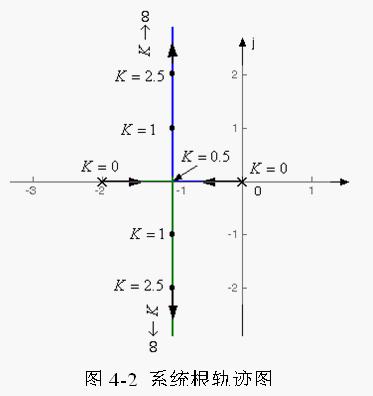
　　利用计算结果在S平面上描点并用平滑曲线将其连接，便得到K^*（或K）从零变化到无穷大时闭环极点在S平面上移动的轨迹，即根轨迹，如图4-2所示。图中，根轨迹用粗实线表示，箭头表示K^*（或K）增大时两条根轨迹移动的方向。

　　在控制系统的分析和综合中，往往只需要知道根轨迹的粗略形状。由相角条件和幅值条件所导出的8条规则，为粗略地绘制出根轨迹图提供方便的途径。

　　在有些情况下，有必要对按基本规则画出的根轨迹的粗略形状，特别是位于虚轴附近的部分，进行修正，使之精确化。实现精确化的一条比较简便的途径，是采用一种由埃文斯设计的所谓对数螺旋尺的专用工具。

　　根轨迹的计算机辅助制图,70年代以来，随着电子计算机的普及，利用计算机对根轨迹的辅助制图的算法和程序都已建立，这大大减轻了系统分析和设计人员的繁重工作。

　　根轨迹的应用主要有三个方面。

　　1.用于分析开环增益(或其他参数)值变化对系统行为的影响：在控制系统的极点中，离虚轴最近的一对孤立的共轭复数极点对系统的过渡过程行为具有主要影响，称为主导极点对。在根轨迹上，很容易看出开环增益不同取值时主导极点位置的变化情况，由此可估计出对系统行为的影响。

　　2.用于分析附加环节对控制系统性能的影响：为了某种目的常需要在控制系统中引入附加环节，这就相当于引入新的开环极点和开环零点。通过根轨迹便可估计出引入的附加环节对系统性能的影响。

　　3.用于设计控制系统的校正装置：校正装置是为了改善控制系统性能而引入系统的附加环节，利用根轨迹可确定它的类型和参数设计。

→如果您认为本词条还有待完善，请编辑词条

词条内容仅供参考，如果您需要解决具体问题
（尤其在法律、医学等领域），建议您咨询相关领域专业人士。本词条对我有帮助0

收藏到:

同义词: 暂无同义词

关于本词条的评论 (共0条）发表评论>>

根轨迹法 发表评论(0) 编辑词条