多元线性回归分析预测法 发表评论(0) 编辑词条
多元线性回归分析预测法概述 编辑本段回目录
在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况。而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。这时采用一元回归分析预测法进行预测是难以奏效的,需要采用多元回归分析预测法。
多元回归分析预测法,是指通过对两上或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时,称为多元线性回归分析。
多元线性回归模型的检验 编辑本段回目录
多元线性回归模型与一元线性回归模型一样,在计算出回归模型之后,要对模型进行各种检验。
多元线性回归模型的检验方法有:判定系数检验(R检验),回归系数显著性检验(T检验),回归方程显著性检验(F检验)。
1、判定系数检验。多元线性回归模型判定系数的定义与一元线性回归分析类似。判定系数R的计算公式为: R = R接近于1表明Y与X1, X2 ,…, Xk之间的线性关系程度密切;R接近于0表明Y与X1, X2 ,…, Xk之间的线性关系程度不密切。
2、回归系数显著性检验。在多元回归分析中,回归系数显著性检验是检验模型中每个自变量与因变量之间的线性关系是否显著。显著性检验是通过计算各回归系数的t检验值进行的。回归系数的t检验值 的计算公式为:= (j = 1,2,…,k),式中 是回归系数 的标准差。在多元回归模型中,某个变量回归系数的t检验没有通过,说明该变量与因变量之间不存在显著的线性相关关系,在回归分析时就可以将该变量删去,或者根据情况作适当的调整,而后用剩下的自变量再进行回归分析。
3、回归方程的显著性检验。回归方程的显著性检验是检验所有自变量作为一个整体与因变量之间是否有显著的线性相关关系。显著性检验是通过F检验进行的。F检验值的计算公式是:F(k ,n-k-1)= 多元回归方程的显著性检验与一元回归方程类似,在此也不再赘述。回归方程的显著性检验未通过可能是选择自变量时漏掉了重要的影响因素,或者是自变量与因变量间的关系是非线性的,应重新建立预测模型。
多元线性回归预测模型的公式 编辑本段回目录
多元线性回归预测模型一般公式为:
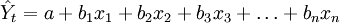
多元线性回归模型中最简单的是只有两个自变量(n=2)的二元线性回归模型,其一般形式为:
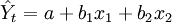
下面以二元线性回归分析预测法为例,说明多元线性回归分析预测法的应用。
二元线性回归分析预测法,是根据两上自变量与一个因变量相关关系进行预测的方法。二元线性回归方程的公式为:
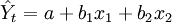 (1)
(1)
式中: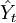 :因变量;
:因变量;
x1,x2:两个不同自变量,即与因变量有紧密联系的影响因素。
a,b1,b2:是线性回归方程的参数。
a,b1,b2是通过解下列的方程组来得到。
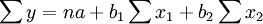
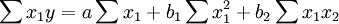 (2)
(2)
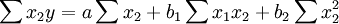
二元线性回归预测法基本原理和步骤同一元线性回归预测法没有原则的区别,大体相同。
相关条目编辑本段回目录
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 多元线性回归分析预测法 F检验 T检验 一元回归分析预测法 一元线性回归分析 一元线性回归模型 一元线性回归预测法 显著性检验 相关分析 线性回归预测 非线性回归预测

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
