转移概率矩阵 发表评论(0) 编辑词条
转移概率矩阵(Transition Probability Matrix)
什么是转移概率矩阵编辑本段回目录
转移概率矩阵:矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,故称为转移概率矩阵。如用于市场决策时,矩阵中的元素是市场或顾客的保留、获得或失去的概率。P(k)表示k步转移概率矩阵。
转移概率矩阵的特征编辑本段回目录
转移概率矩阵的分析 编辑本段回目录
所谓矩阵,是指许多个数组成的一个数表。每个数称为矩阵的元素。矩阵的表示方法是用括号将矩阵中的元素括起来,以表示它是一个整体。如A就是一个矩阵。
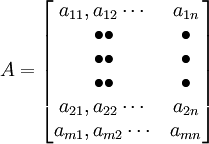
这是一个由m行n列的数构成的矩阵, 表示位于矩阵中第i行与第j列交叉点上的元素, 矩阵中的行数与列数可以相等,也可以不等。当它们相等时,矩阵就是一个方阵。
由转移概率组成的矩阵就是转移概率矩阵。也就是说构成转移概率矩阵的元素是一个个的转移概率。
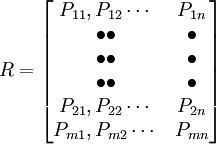
转移概率与转移概率矩阵编辑本段回目录
假定某大学有1万学生,每人每月用1支牙膏,并且只使用“中华”牙膏与“黑妹”牙膏两者之一。 根据本月(12月)调查,有3000人使用黑妹牙膏,7000人使用中华牙膏。 又据调查,使用黑妹牙膏的3000人中, 有60%的人下月将继续使用黑妹牙膏, 40%的人将改用中华牙膏; 使用中华牙膏的7000人中, 有70%的人下月将继续使用中华牙膏, 30%的人将改用黑妹牙膏。据此,可以得到如表-1所示的统计表。
表-1 两种牙膏之间的转移概率
拟用 黑妹牙膏 中华牙膏 现用 黑妹牙膏 60% 40% 中华牙膏 70% 30%
上表中的4个概率就称为状态的转移概率,而这四个转移概率组成的矩阵
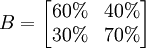
称为转移概率矩阵。可以看出, 转移概率矩阵的一个特点是其各行元素之和为1。 在本例中,其经济意义是:现在使用某种牙膏的人中,将来使用各种品牌牙膏的人数百分比之和为1。
2. 用转移概率矩阵预测市场占有率的变化
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
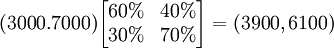
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。
假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
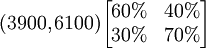
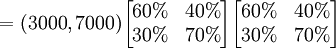
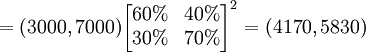
这里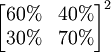 称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
参考文献编辑本段回目录
相关条目编辑本段回目录
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 转移概率矩阵 决策 市场 矩阵 转移概率 顾客 马尔可夫过程

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
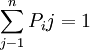 ,即矩阵中每一行
,即矩阵中每一行