等可能性决策法 发表评论(0) 编辑词条
等可能性决策法也称等可能性法、拉普拉斯决策准则、拉普拉斯方法
等可能性决策法概述 编辑本段回目录
等可能性决策是当决策人在决策过程中,不能肯定哪种状态容易出现,哪种状态不容易出现时,可以一视同仁,认为各种状态出现的可能性是相等的。如果有 n个自然状态,那么每个自然状态出现的概率即为 ,然后按收益最大的或损失最小的期望值(或矩阵法)进行决策。这个想法是法国数学家皮埃尔-西蒙·拉普拉斯(Pierre Simon Laplace;1749~1827)首先提出的,所以又叫作拉普拉斯方法。
,然后按收益最大的或损失最小的期望值(或矩阵法)进行决策。这个想法是法国数学家皮埃尔-西蒙·拉普拉斯(Pierre Simon Laplace;1749~1827)首先提出的,所以又叫作拉普拉斯方法。
等可能性决策法的基本原理 编辑本段回目录
等可能性决策法是当存在两种或两种以上的可行方案时,假定每一种方案遇到各种自然状态的可能性是相等的,然后求出各种方案的损益期望值,以此作为依据,进行决策;这种决策方法带有一定的主观性。
等可能性决策法的操作步骤 编辑本段回目录
等可能性决策法的基本操作步骤
以 为各状态出现的概率,求出方案的期望值 E(A1)如下:
为各状态出现的概率,求出方案的期望值 E(A1)如下:
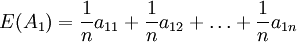
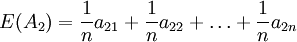

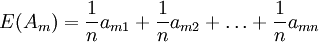
然后取max{E(A1)}(i=1,2,…,m)为决策者的目标值。
若有两个以上方案的期望值相等,则再比较这些方案的D(A1),D(A1) = E(A1) − min(aij),取 D(A1)值最小的那一个方案。
等可能性决策法的应用领域 编辑本段回目录
等可能性决策法的主要应用领域:
等可能性决策法主要应用于生产、销售、建筑施工和交通运输等领域,在决策者无法预测各种自然状态出现的概率时,认为各种状态出现的概率相等,但每种状态下各方案的损益值是可以预测的,在这种情况下,可以使用等可能性决策法。4.实用案例今有五个行动方案 A1,A2,A5,四个自然状态%1,%2,%3,%4(它们出现的概率不知道),其相应的效益值列于下表:
决策表如下: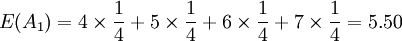
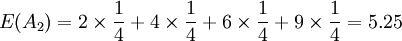
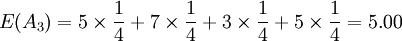
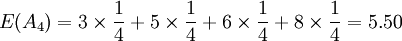
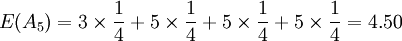
因为 E(A) = E(A4),所以要比较 D(A1)和 D(A4)的大小。
D(A1) = E(A1) − min(aij) = 5.50 − 4 = 1.50
D(A4) = E(A4) − min(a4j) = 5.50 − 3 = 2.50
因为D(A1) < D(A4),所以选取方案 A1。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
2
标签: 等可能性决策法 Pierre Simon Laplace 决策 皮埃尔-西蒙·拉普拉斯

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条


