子博弈精炼纳什均衡 发表评论(0) 编辑词条

完全信息动态博弈——子博弈精炼纳什均衡（subgame perfect Nash equilibrium）

　　子博弈精炼纳什均衡的创立者. ——1994年诺贝尔经济学奖获奖者、莱茵哈德·泽尔腾(Reinhard Selten).

　　泽尔腾则在60年代中期将纳什均衡概念引入动态分析。在1965年发表《需求减少条件下寡头垄断模型的对策论描述》一文，提出了“子博弈精炼纳什均衡”的概念，又称“子对策完美纳什均衡”。这一研究对纳什均衡进行了第一次改进，选择了更具说服力的均衡点。海萨尼在60年代末把不完全信息引入博弈分析。

　　将纳什均衡中包含的不可置信的威胁策略剔除出去。它要求参与者的决策在任何时点上都是最优的，决策者要“随机应变”，“向前看”，而不是固守旧略。

　　由于剔除了不可置信的威胁，在许多情况下，精炼纳什均衡也就缩小了纳什均衡的个数。这一点对预测分析是非常有意义的。

　　用动态博弈理论来讨论实际究竟发生哪个纳什均衡。

　　给定“历史”，每一个行动选择开始至博弈结束构成了一个博弈，称为“子博弈”。

　　只有当参与人的策略在每一个子博弈中都构成纳什均衡叫做精炼纳什均衡。或者说，组成精炼纳什均衡的策略必须在每一个子博弈中都是最优的。

　　子博弈:一个扩展式表示博弈的子博弈G是由一个单结信息集x开始的与所有该决策结的后续结(包括终点结)组成的能自成一个博弈的原博弈的一部分。

　　对于扩展式博弈的策略组合S*=(S1*,…,Si*,…,Sn*) ,如果它是原博弈的纳什均衡;它在每一个子博弈上也都构成纳什均衡,则它是一个子博弈精炼纳什均衡。

　　博弈论专家常常使用“序惯理性”(Sequential rationality)：指不论过去发生了什么，参与人应该在博弈的每个时点上最优化自己的策略。子博弈精练纳什均衡所要求的正是参与人应该是序惯理性的。对于有限完美信息博弈，逆向归纳法是求解子博弈精炼纳什均衡的最简便的方法。因为有限完美信息博弈的每一个决策结都开始一个子博弈。求解方法：　最后一个结点上的子博弈（纳什均衡）→倒数第二个（纳什均衡） → ······ → 初始结点上的子博弈（纳什均衡）。

　　动态是世间万物的基本特征。完全信息静态博弈只是一种独特的理想状态。在现实中，当后一个参与人行动时，自然会根据前者的选择而调整自己的选择，而前者也会理性地预期到这一点，所以不可能不考虑自己的选择对他人的影响。1965年，泽尔腾通过对动态博弈的分析，提出了“子博弈精炼纳什均衡”的概念，它要求任何参与人在任何时间、地点的决策都是最优的，决策者应该随机应变，而不是固守前谋。这就推导出子博弈的概念。当参与人的战略在每一个子博弈中都构成纳什均衡时，则形成“子博弈精炼纳什均衡”。也就是说，组成“子博弈精炼纳什均衡”的战略必须在每一个子博弈中都是最优的。

　　子博弈精炼纳什均衡用于区分动态博弈中的"合理纳什均衡"与"不合理纳什均衡",将纳什均衡中包含有不可置信威胁策略的均衡剔除出去,就是说,使最后的均衡中不再包含有不可置信威胁策略的存在。

　　逆向归纳法（Backward Induction）是求解子博弈精炼纳什均衡的最简便方法。在求解子博弈精炼纳什均衡时,从最后一个子博弈开始逆推上去,这就是逆向归纳法。所以逆向归纳法就是从动态博弈的最后一个阶段或最后一个子博弈开始,逐步向前倒推以求解动态博弈均衡的方法。

　　用逆向归纳法求解子博弈精炼纳什均衡；承诺行动与子博弈精炼纳什均衡；逆向归纳法与子博弈精炼均衡存在的问题。

　　在表1描述的博弈模型中，每一次微观主体间的博弈均可看作一个子博弈。子博弈精炼纳什均衡包含两层含义:

　　（1）它是原博弈的纳什均衡；

　　（2）它在每一个子博弈上给出纳什均衡。

　　子博弈精炼纳什均衡就是要剔除那些只在特定情况下是合理的，而在其他情况下并不合理的行动规则。

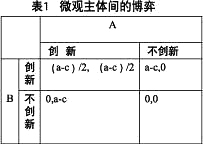
　　表１　微观主体间的博弈

　　在表1中，a代表只有一个微观主体创新时所带来的收益，c代表该微观主体创新所需付出的成本。当只有一个微观主体进行创新时将会获得创新带来的全部收益（a-c），而当两个主体同时创新时，收益将会减半(a-c)/2。一般情况下“a-c>0”，则很明显在这个博弈过程中，（创新，创新）是一个纳什均衡，更严格地说，是一个严格优势策略均衡。依此类推，可以得出，在每一次新的金融规制后，（创新，创新）这个策略都将是至下次新规制出现前的子博弈的纳什均衡。因此，在利润的驱动下，微观主体都会选择创新这样一个策略。

　　举例的进一步分析

　　在市场进入博弈中，在给定企业B已经进入的情况下，在位者的“斗争”，“高价”策略已不再是最优的，这种“斗争”是不可置信的威胁，因为斗争的结果是没有利润；而合作会带来50单位利润。所以，（进入，高价）不是一个精炼纳什均衡。剔除这个均衡，可以证明，（进入，高价）是唯一的子博弈精炼纳什均衡。

　　在动态博弈中，参与人的行动有先后顺序，后行动的参与人在自己行动之前就可以观察到先行动者（参与人）的行为，并在此基础上选择相应的策略。而且，由于先行动者拥有后行动者可能选择策略的完全信息，因而先行动者在选择自己的策略时，就可以预先考虑自己的选择对后行动者选择的影响，并采取相应的对策。

　　利用房地产开发的例子，讨论子博弈精炼纳什均衡。表２给出了静态条件下双方参与人的收益情况。

　　表2　房地产开发博弈（静态）的收收益矩阵

　　从表２可以知道，该博弈有两个纳什均衡，即（Ａ开发，Ｂ不开发）和（Ａ不开发，Ｂ开发），我们无法确定是开发商Ａ选择开发，开发商Ｂ选择不开发，还是恰恰相反的结果。

　　现在，我们讨论动态博弈。假定房地产开发商Ａ是先行动者。在行动之前，开发商Ａ对对手开发商Ｂ的策略进行了预测。在行动开始之前的Ａ看来，如果不计得失，Ｂ有四种策略可供选择：

　　策略一：无论Ａ是否选择开发，Ｂ选择开发。

　　策略二：若Ａ选择开发，Ｂ也选择开发；若Ａ选择不开发，Ｂ也选择不开发。

　　策略三：若Ａ选择开发，Ｂ就选择不开发；若Ａ选择不开发，Ｂ就选择开发。

　　策略四：无论Ａ是否选择开发，Ｂ都选择不开发。

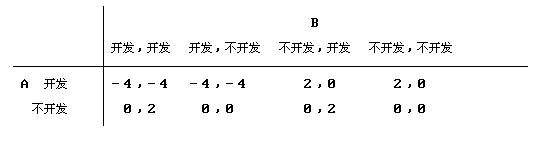
　　在表２的基础上，结合Ａ先行动，Ｂ可能选择的四种策略，不难得出表3。

　　表3　　先行动者Ａ对Ｂ预测结果的收益矩阵

　　由表3可以看出，在开发商Ａ先行动的情况下，开发商Ｂ可供选择的策略中，策略一只包括了上述两个纳什均衡中的后一种均衡，即（Ａ不开发，Ｂ开发），而没有包括前一种纳什均衡，即（Ａ开发，Ｂ不开发）；策略二上述两种纳什均衡都没有包括；策略四只包括了上述两种纳什均衡中的前一种均衡，即（Ａ开发，Ｂ不开发），而未包括后一种纳什均衡，即（Ａ不开发，Ｂ开发）；只有策略三既包括了上述两种纳什均衡中的前一种均衡，又包括了后一种均衡。也就是说，如果Ｂ选择策略三，那么，无论Ａ作出什么选择，Ｂ的回应都能达到纳什均衡。反过来，在给定Ｂ会选择策略三来回应Ａ的选择的前提下，开发是Ａ的占优选择。因此，Ａ一定会选择开发