模糊综合评价模型 发表评论(0) 编辑词条
模糊综合评价模型(Fuzzy Synthetic Evaluation Model)
什么是模糊综合评价模型? 编辑本段回目录
模糊综合评价方法是模糊数学中应用的比较广泛的一种方法。在对某一事务进行评价时常会遇到这样一类问题,由于评价事务是由多方面的因素所决定的,因而要对每一因素进行评价;在每一因素作出一个单独评语的基础上,如何考虑所有因素而作出一个综合评语,这就是一个综合评价问题。
模糊评价的基本思想 编辑本段回目录
许多事情的边界并不十分明显,评价时很难将其归于某个类别,于是我们先对单个因素进行评价,然后对所有因素进行综合模糊评价,防止遗漏任何统计信息和信息的中途损失,这有助于解决用“是”或“否”这样的确定性评价带来的对客观真实的偏离问题。
模糊综合评价模型类别 编辑本段回目录
模糊评价基本模型
设评判对象为P: 其因素集 ,评判等级集
,评判等级集 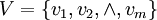 。对U中每一因素根据评判集中的等级指标进行模糊评判,得到评判矩阵:
。对U中每一因素根据评判集中的等级指标进行模糊评判,得到评判矩阵:
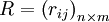 (1)
(1)
其中,rij表示ui关于vj的隶属程度。(U,V,R) 则构成了一个模糊综合评判模型。确定各因素重要性指标(也称权数)后,记为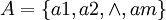 ,满足
,满足 ,合成得
,合成得
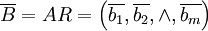 (2)
(2)
经归一化后,得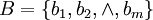 ,于是可确定对象P的评判等级。
,于是可确定对象P的评判等级。
置信度模糊评价模型
(1) 置信度的确定。
在(U,V,R)模型中,R中的元素rij 是由评判者“打分”确定的。例如 k 个评判者,要求每个评判者uj 对照 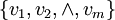 作一次判断,统计得分和归一化后产生
作一次判断,统计得分和归一化后产生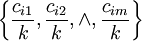 , 且
, 且 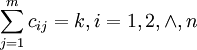 , 组成 R0 。 其中
, 组成 R0 。 其中 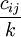 既代表 uj 关于vj 的“隶属程度”,也反映了评判uj 为 vj 的集中程度。数值为1 ,说明 uj 为 vj 是可信的,数值为零为忽略。因此,反映这种集中程度的量称为“置信度”。
既代表 uj 关于vj 的“隶属程度”,也反映了评判uj 为 vj 的集中程度。数值为1 ,说明 uj 为 vj 是可信的,数值为零为忽略。因此,反映这种集中程度的量称为“置信度”。
使用AHP法确定指标权重,之后作关于权数的等级划分,由此决定其结果的信度。当取 N 个等级时,其量化后对应于[0,1]区间上N次平分。对某 j 个指标,取遍 k 个专家对该指标评估所得的权重,得![\left[ a_{1j} , a_{2j}, \land , a_{kj} \right]](Article/UploadFiles/200908/2009082412281145.png) 。作和式
。作和式
![\sum ^N_{i=1} {d_{ij} \over k } \left[ a_i ,b_i \right] \underline{\Delta} \left[a^j, b^j \right]](Article/UploadFiles/200908/2009082412281206.png) (3)
(3)
其中dij 表示数组中![\left[ a_{1j} , a_{2j} , \land , a_{kj} \right]](Article/UploadFiles/200908/2009082412281145.png) 属于
属于![\left[a_i , b_i \right]](Article/UploadFiles/200908/2009082412281211.png) 的个数,a0 = 0,bN = 1。
的个数,a0 = 0,bN = 1。
取 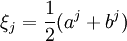 (4)
(4)
取遍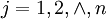 , 得
, 得 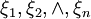 ,归一化后得到权向量
,归一化后得到权向量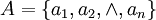 。如果
。如果 ![\xi_j \in [a_i, b_i]](Article/UploadFiles/200908/2009082412281316.png) 则 ai 的信度为
则 ai 的信度为 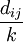 。由此得信度向量为
。由此得信度向量为 。
。
(2)置信度的综合
设c1,c2 是二个置信度,对于逻辑AND,其信度合成为
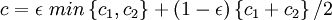 (5)
(5)
对于逻辑OR, 信度成为
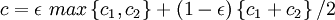 (6)
(6)
其中 ![\epsilon \in [0,1]](Article/UploadFiles/200908/2009082412281410.png) 为参数,可适当配置。(5)、(6)二式的含义是:在逻辑 AND 下,
为参数,可适当配置。(5)、(6)二式的含义是:在逻辑 AND 下, 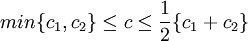 ; 在逻辑 OR 下,
; 在逻辑 OR 下,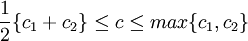 。若
。若 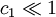 或
或 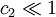 , 则 (5)、(6) 二式中的平均值补偿部分不宜太强。 ε 可如下配置:
, 则 (5)、(6) 二式中的平均值补偿部分不宜太强。 ε 可如下配置:
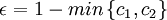 (7)
(7)
对于(2)信度合成为:
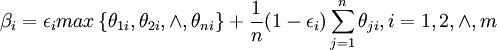 (8)
(8)
其中,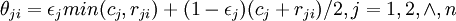 (9)
(9)
εi 和 εj 的选择可参照(7)。
结合(2),得到信度的评判结果:
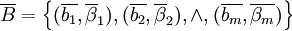 (10)
(10)
模糊综合评价模型的运用 编辑本段回目录
对于企业的财务危机状况,其影响因素具有极大的复杂性,精确化能力的降低造成对系统描述的模糊性,运用模糊手段来处理模糊性问题,将会使评价结果更真实、更合理。模糊综合评价模型的建立须经过以下步骤:
1、给出备择的对象集:这里即为各上市公司;
2、确定指标集:即把能预测财务危机的主要财务比率构成一个集合;
3、建立权重集:由于指标集中各指标的重要程度不同,所以要对一级指标和二级指标分别赋予相应的权数。第一层次的权重集 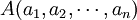 ,第二层次的权重集
,第二层次的权重集  。这里将采用因子分析法确定权数;
。这里将采用因子分析法确定权数;
4、确定评语集: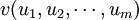 ,我们把评价集设为v={安全,一般,危险};
,我们把评价集设为v={安全,一般,危险};
5、找出评判矩阵: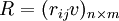 ,首先确定出U对v的隶属函数,然后计算出股票评价指标对各等级的隶属度 rij;
,首先确定出U对v的隶属函数,然后计算出股票评价指标对各等级的隶属度 rij;
6、求得模糊综合评判集 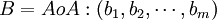 ,即普通的矩阵乘法,根据评判集得终评价结果。
,即普通的矩阵乘法,根据评判集得终评价结果。
业绩评价的模糊模型包含这么几个部分:一是由评价指标体系构成的因素论城;二是由表明隶属度的模糊因子构成的模糊向量;三是用来对单个因素进行评价的评语论城;四是将模糊关系矩阵与模糊向量结合起来的合成算子(普通乘法和有界和不失为一种好的合成算子);四是与模糊评语等级相关的薪酬向量。其基本步骤是:
1、确定评价因素论城,即用什么样的指标来评价或评价者关注什么方面的内容;
2、确定评语论城,即就单个因素而言,评价者对被评价因素有什么样的判断或以什么方式表示评价结果;
3、确定模糊向量,即我们对每个因素的重视程度;
4、先对单个因素进行评价,就会得到一个因素与评语之间的模糊关系矩阵;
5、采用某个合成算子,对模糊关系矩阵与模糊向量进行合成,这里采用普通乘法和有界和得到综合模糊评价结果;
6、设与评语论对应的薪酬矩阵为C,得出代理人应得报酬。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 模糊综合评价模型 AHP法 上市公司 业绩评价 权重 统计信息 股票 评价指标 财务危机 财务比率 因子分析法

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
