基数效用论 发表评论(0) 编辑词条
基数效用论概述 编辑本段回目录
西方经济学效用理论的思想渊源,也许可以追溯到以边沁和密尔为代表的英国功利主义哲学,但其直接奠基却是产生于19世纪50-70年代的“边际革命”。在此期间,德国的戈森、英国的杰文斯、奥地利的门格尔以及法国的瓦尔拉斯等人差不多同时,但又都各自独立地发现了“边际效用递减规律”。边际效用学说建立在效用可以直接计量的假设之上,因此也被称为“基数效用论”。
基数效用论是19世纪和20世纪初期西方经济学普遍使用的概念。其基本观点是:效用是可以计量并可以加总求和的。表示效用大小的计量单位被称为效用单位(Utility unit)。因此,效用的大小可以用基数(1、2、3……)来表示,正如长度单位可以用米来表示一样。基数效用论采用的是边际效用分析法。基数效用论认为效用大小是可以测量的,其计数单位就是效用单位。
基数效用论认为,商品的边际效用是递减的。而马歇尔指出,货币也必须服从边际效用递减规律。既然如此,由于富人持有的货币量大于穷人,所以前者的边际效用小于后者。如果把一元钱从富人那里转移到穷人那里,整个社会的效用就会增加。所以,边际效用递减规律可以成为收入平均化的理论依据。
基数效用论的假设条件 编辑本段回目录
1、效用量可以具体衡量;
2、边际效用(MU)递减规律。
基数效用论与序数效用论的异同 编辑本段回目录
区别
基数效用论采用边际效用的分析法。而序数效用论采用无差异曲线分析法来考察消费者行为,并在此基础上推导需求曲线。物的效用向量可以表示为:Ux=U(x1, x2, x3, …, xn)。向量的模长可以直接比较,这是基数效用论的方法;多个向量可以复合成一个总的向量,或者一个总的向量可以分解成多个、多组向量,这是序数效用论的方法。下表给出两种理论的具体区别:
| 效用理论类型 | 主要观点 | 假设条件 | 分析工具 | 经济学家 |
|---|---|---|---|---|
| 基数效用论 | 效用可计量 | 苛刻 | 边际效用 | 马歇尔 |
| 序数效用论 | 效用可比较 | 宽松 | 无差异曲线 | 希克斯 |
联系
基数效用论和序数效用论,是消费者行为理论中两个重要的理论。序数效用论的缘起,在于分析效用会相互影响的不同商品之间的关系(由Jevons等人的边际革命所推广的基数效用论一开始假设商品之间的效用没有相互影响,因而无法研究有关联的商品之间的关系,于是Pareto从Edgeworth那里借用了无差异曲线,用以说明两种商品之间的关系)。从这里可以知道,无差异曲线最早是从效用曲线得来的,而效用曲线本来是基数效用论中的概念。
边际效用递减规律 编辑本段回目录
在一定时间内,在其他商品的消费数量保持不变的条件下,随着消费者对某种商品消费量的增加,消费者从该商品连续增加的每一消费单位中所得到的效用增量即边际效用是递减的。
例如:如下表所示,在一个人很饥饿的时候,吃第一个包子给他带来的效用是很大的,以后,随着这个人吃的包子数量的边续增加,虽然总效用不断增加,但每一个包子给他带来的效用增量即边际效用却是递减的。当他完全吃饱的时候,包子的总效用达到最大值,而边际效用却降为零。如果他还继续吃包子,就会感到不适,这意味着包子的边际效用进一步降为负值,总效用也开始下降。
| 包子 | 总效用(TU) | 边际效用(MU) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | -2 |
1、边际效用递减规律的推导
把效用看作消费的变量,据此构建的效用函数为:
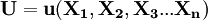 (1)
(1)
式中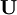 表示消费者一定时期内获得的效用总量,
表示消费者一定时期内获得的效用总量,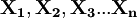 表示,
表示,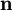 种消费品的消费数量。假定式(1)是一个连续、可微的凹函数,即:
种消费品的消费数量。假定式(1)是一个连续、可微的凹函数,即:
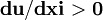 ,且
,且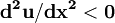 (2)
(2)
式中 ,记
,记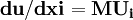 ,称为
,称为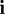 种消费品的边际效用;式(2)的含义为“一个消费者从同一种消费品中获得的效用总量以递减的速率递增”或“一个消费者从同一种消费品每一单位的增量中所获得的效用是递减的”,这就是所谓的“边际效用递减规律”。
种消费品的边际效用;式(2)的含义为“一个消费者从同一种消费品中获得的效用总量以递减的速率递增”或“一个消费者从同一种消费品每一单位的增量中所获得的效用是递减的”,这就是所谓的“边际效用递减规律”。
假定消费者在一定收入水平下总是购买效用最大的消费品组合,则消费者的行为可以转化为一个求解效用函数条件极值的数学问题。设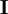 为消费者的收入,
为消费者的收入,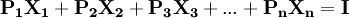 为
为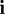 种消费品的价格,则
种消费品的价格,则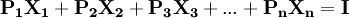 为消费者的预算约束,以此条件求效用函数(1)的最大值,得:
为消费者的预算约束,以此条件求效用函数(1)的最大值,得:
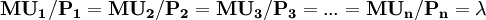
式中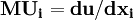 ,即
,即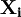 的边际效用;
的边际效用;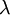 为货币收入的边际效用。
为货币收入的边际效用。
2、对边际效用递减规律的解释
- 生理或者心理上的原因:重复刺激;
- 商品本身用途的多样性:先重后轻。
附件列表
→如果您认为本词条还有待完善,请 编辑词条
词条内容仅供参考,如果您需要解决具体问题
(尤其在法律、医学等领域),建议您咨询相关领域专业人士。
0
标签: 基数效用论 Pareto 密尔 序数效用论 戈森 效用 效用曲线 效用理论 无差异曲线 杰文斯 消费者行为理论

同义词: 暂无同义词
关于本词条的评论 (共0条)发表评论>>
 编辑实验
创建词条
编辑实验
创建词条
