OMD模型 发表评论(0) 编辑词条

序值均差模型(Ordered Mean Difference，简称OMD模型)

　　OMD模型由Roger.J.Bowden在2000年提出。该模型可用于评价基金绩效、套利策略、免疫策略、投资组合增强策略等方面的研究。这里介绍其在基金绩效评价中的研究。评价基金绩效中，OMD模型的优点在于不需要CAPM模型的严格假设条件，并且由于该模型的非参数估计特性，它对基金和市场收益率的概率分布没有正态分布或对称分布的要求。

　　引入序值均差值模型评价基金绩效,解决了传统基金绩效评价指标在使用中的局限性,可以满足投资者的个性化投资需求,这里又通过实证分析了同一家基金管理公司不同投资风格的三只基金的市场表现,并通过对比分析了该指标相对于传统指标在评价中的优越性。

1、等价边际

　　构造一个投资组合，待评价基金(收益率为γ)和市场基准组合(收益率为R)的投资比例分别为x和(1-x)。若投资者具有冯·诺依曼—摩根斯坦效用函数U(·)，则最优组合应满足

　　maxE_r,R[U(xr + (1 − x)R)] (1)

　　在使用等价边际指标评价基金绩效时，我们以(r-t)代替r表示一只基金的收益率，其中t可以看作是从由于基金经理人拥有的市场时机选择能力而获得的超额利润中抽取的佣金。如果购买一只基金，由于t的存在会使基金的实际收益率降低，而且随着t的增加，投资者会减少对该基金的持有量，最终减少为零。从另一个角度看，投资者能够接受的t越高，则该基金的绩效越好，换句话说较高的t表示对基金经理人特有的市场时机选择能力评价较高。这里的t就是等价边际。值得注意的是，这种评价体现了等价边际这一评价指标个性化的一面，即可以是任意投资者的主观评价。

　　等价边际的定义式为:

　　如果投资者是厌恶风险的，即效用函数为凹函数，则最优投资组合应满足上式的一阶条件：

E(r − R − t)U'[x(r − t) + (1 − x)R]) = 0

令x=0，可以得到等价边际指标

　　(2)

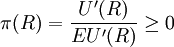且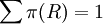

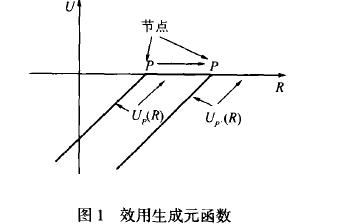
2、效用生成元

　　计算等价边际的最大难点在于投资者效用函数的确定。为此，我们构造一种具有特殊形式的效用函数一效用生成元。该函数具有一种特殊的形式，如图1所示。效用生成元有两段线性部分组成，节点为收益率P。我们可以把P看作是“目标收益率”，即投资者更关注的是回报率能否达到该值，而不在意收益率超过该值后的情况。因此P点反映了不同投资者的风险厌恶程度：随着P点的右移，投资者的风险厌恶程度低。通常情况下，P>0。

　　对于一个固定值P，效用生成元函数为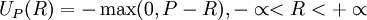：可以证明，具有任意风险特征的投资者的效用函数都可以分解为一组具有不同P点的，即不同风险厌恶程度的效用生成元的加权集合。例如，一个风险厌恶的投资者的效用函数中，具有较低P值的效用生成元在该投资者的效用函数中具有较高的权重。

3、OMD样本函数

　　既然具有任意形式的效用函数都可以分解为效用生成元函数Up(R)的加权集合，那么如果可以计算出效用生成元函数在P点的等价边际(记为t_p或t(P))，则通过相同的方法就可以求出任意效用函数的等价边际t_U我们称t(P)为OMD样本函数，定义为：

　　,

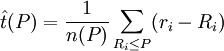其中 n(P)={#Ri≤P} (2)

　　根据市场基准收益率和t(P)可以绘制基金的OMD曲线。如果待评定基金的OMD曲线总是位于的上方，可以说对于具有任何风险特征的投资者该基金对于市场基准投资组合都是占优的，或者说基金经理人具有较好的市场时机选择能力和选股能力。

　　由于OMD函数具有非参数特性，不需要对收益率分布做任何假设，也不用对证券价值进行评估，更回避了CAPM模型有效性的问题，因此在一定程度上优于传统的基金绩效评价指标。

1、研究对象与数据处理

　　自2001年9月我国证券市场上发行第一只开放式基金——华安创新基金，到2004年8月底已累计达到100只。为了便于比较，从中选取同一家基金公司的三只基金进行分析，分别是招商安泰股票证券投资基金、平衡型证券投资基金和债券证券投资基金，数据从2003年6月2日至2004年8月30日，共300个日数据。对每个日数据，基金的资产净值由下式计算：

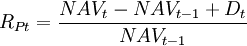
式中：R_Pt为基金在t日的收益率；NAVt为第t日的 基金净资产；Dt为基金在t日的现金分红。

　　根据我国《证券投资基金管理暂行办法》关于基金投资于股市不得高于总投资额的80％，投资于债券、现金持有不得低于20％ 的规定，我们选择上证180指数作为股票市场综合指数，上证国债指数作为国债市场的综合指数，两者分别以0.8和0.2的权重加权平均,来计算市场基准收益率，即市场基准收益率=80％×上证180指数收益率+20％×上证国债指数收益率

2、对三只证券投资基金的实证分析

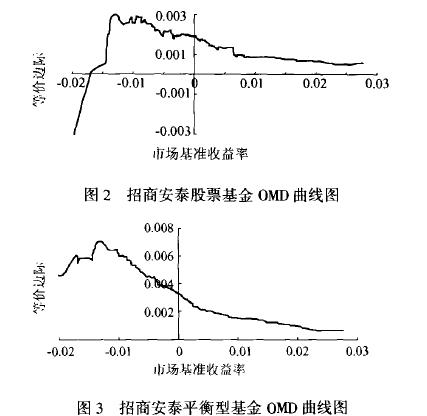
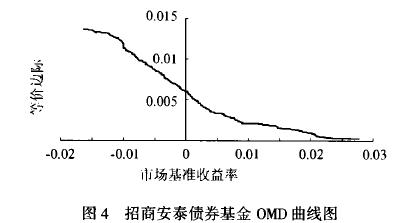
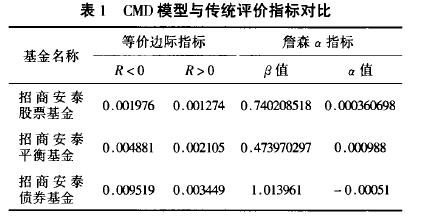
　　(1) OMD曲线图及分析

　　从图2～图4中可以看出，平衡型和债券基金的OMD曲线在样本区间内位于水平轴上方，说明这两只基金优于市场基准组合，或者其基金经理人具有较好的市场时机选择能力和选股能力。值得注意的是，当市场基准收益率R为负值时，等价边际t_U，具有较高的正值，而在市场收益较高的区域内，等价边际t_U“迅速”降低，尤其是债券基金下降幅度大、速率快。说明在市场走低的情况下，投资目标为追求稳定收益、规避市场价格波动风险的平衡型和债券基金仍维持良好的市场表现，但是市场形势转好，这两只基金的表现不如追求较高收益率的股票基金。

　　(2)OMD模型等价边际指标与传统评价指标比较分析

　　在三种传统评价指标中，我们选择了詹森α指数与等价边际进行绩效评价比较，计算结果如表1所示。

　　可以看出，当使用等价边际指标评价基金业绩表现良好时，詹森α指标对基金的表现评价不高，尤其是对债券基金出现α<0的情况，表明该基金位于证券市场先下方，即基金业绩劣于市场基准投资组合。这主要是因为Jensen指数是在CAPM模型上提出来的，假定基金的β系数固定，但是由于基金经理人的市场时机选择能力和择股能力不同，因而会引起导致变动的非线性变化，也就是说当基金经理具有优良的时机选择能力时，使用该指标可能会低估基金的业绩。而且在使用Jensen指数评估基金整体绩效时，隐含了非系统风险已被彻底分散掉的假设，如果没有完全消除非系统风险，则Jensen指数可能给出错误信息。这也从另一个角反映了使用等价边际指标评价基金业绩时可以避免上述问题。