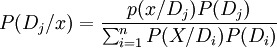贝叶斯 发表评论(0) 编辑词条

　　贝叶斯(1702-1763) Thomas Bayes，英国数学家.1702年出生于伦敦，做过神甫。1742年成为英国皇家学会会员。1763年4月7日逝世。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论，并创立了贝叶斯统计理论，对于统计决策函数、统计推断、统计的估算等做出了贡献.1763年发表了这方面的论著，对于现代概率论和数理统计都有很重要的作用。贝叶斯的另一著作《机会的学说概论》发表于1758年。贝叶斯所采用的许多术语被沿用至今。
　　贝叶斯决策理论是主观贝叶斯派归纳理论的重要组成部分。
　　贝叶斯决策就是在不完全情报下，对部分未知的状态用主观概率估计，然后用贝叶斯公式对发生概率进行修正，最后再利用期望值和修正概率做出最优决策。
　　贝叶斯决策理论方法是统计模型决策中的一个基本方法，其基本思想是：
　　1、已知类条件概率密度参数表达式和先验概率。
　　2、利用贝叶斯公式转换成后验概率。
　　3、根据后验概率大小进行决策分类。
　　他对统计推理的主要贡献是使用了"逆概率"这个概念，并把它作为一种普遍的推理方法提出来。贝叶斯定理原本是概率论中的一个定理，这一定理可用一个数学公式来表达，这个公式就是著名的贝叶斯公式。 贝叶斯公式是他在1763年提出来的：
　　假定B1,B2,……是某个过程的若干可能的前提，则P(Bi)是人们事先对各前提条件出现可能性大小的估计，称之为先验概率。如果这个过程得到了一个结果A，那么贝叶斯公式提供了我们根据A的出现而对前提条件做出新评价的方法。P(Bi∣A)既是对以A为前提下Bi的出现概率的重新认识，称 P(Bi∣A)为后验概率。经过多年的发展与完善，贝叶斯公式以及由此发展起来的一整套理论与方法，已经成为概率统计中的一个冠以“贝叶斯”名字的学派，在自然科学及国民经济的许多领域中有着广泛应用。

　　设D1，D2，……，Dn为样本空间S的一个划分，如果以P(Di)表示事件Di发生的概率，且P(Di)>0(i=1，2，…，n)。对于任一事件x，P(x)>0，则有：
　　n
　　P(Dj/x)=p(x/Dj)P(Dj)/∑P(X/Di)P(Di)
　　i=1
　　贝叶斯公式

　　（1）如果我们已知被分类类别概率分布的形式和已经标记类别的训练样本集合，那我们就需要从训练样本集合中来估计概率分布的参数。在现实世界中有时会出现这种情况。（如已知为正态分布了，根据标记好类别的样本来估计参数，常见的是极大似然率和贝叶斯参数估计方法）
　　（2）如果我们不知道任何有关被分类类别概率分布的知识，已知已经标记类别的训练样本集合和判别式函数的形式，那我们就需要从训练样本集合中来估计判别式函数的参数。在现实世界中有时会出现这种情况。（如已知判别式函数为线性或二次的，那么就要根据训练样本来估计判别式的参数，常见的是线性判别式和神经网络）
　　（3）如果我们既不知道任何有关被分类类别概率分布的知识，也不知道判别式函数的形式，只有已经标记类别的训练样本集合。那我们就需要从训练样本集合中来估计概率分布函数的参数。在现实世界中经常出现这种情况。（如首先要估计是什么分布，再估计参数。常见的是非参数估计）
　　（4）只有没有标记类别的训练样本集合。这是经常发生的情形。我们需要对训练样本集合进行聚类，从而估计它们概率分布的参数。（这是无监督的学习）
　　（5）如果我们已知被分类类别的概率分布，那么，我们不需要训练样本集合，利用贝叶斯决策理论就可以设计最优分类器。但是，在现实世界中从没有出现过这种情况。这里是贝叶斯决策理论常用的地方。
　　问题：假设我们将根据特征矢量x 提供的证据来分类某个物体，那么我们进行分类的标准是什么？decide wj， if（p(wj|x)>p(wi|x)）(i不等于j)应用贝叶斯展开后可以得到p(x|wj)p(wj)>p(x|wi)p(wi)即或然率p(x|wj)/p(x|wi)>p(wi)/p(wj)，决策规则就是似然率测试规则。
　　结论：对于任何给定问题，可以通过似然率测试决策规则得到最小的错误概率。这个错误概率称为贝叶斯错误率，且是所有分类器中可以得到的最好结果。最小化错误概率的决策规则就是最大化后验概率判据。

　　贝叶斯决策理论方法是统计模式识别中的一个基本方法。贝叶斯决策判据既考虑了各类参考总体出现的概率大小，又考虑了因误判造成的损失大小，判别能力强。贝叶斯方法更适用于下列场合：
　　(1) 样本(子样)的数量(容量)不充分大，因而大子样统计理论不适宜的场合。
　　(2) 试验具有继承性，反映在统计学上就是要具有在试验之前已有先验信息的场合。用这种方法进行分类时要求两点： 第一，要决策分类的参考总体的类别数是一定的。例如两类参考总体(正常状态Dl和异常状态D2)，或L类参考总体D1，D2，…，DL(如良好、满意、可以、不满意、不允许、……)。
　　第二，各类参考总体的概率分布是已知的，即每一类参考总体出现的先验概率P(Di)以及各类概率密度函数P(x／Di)是已知的。显然，0≤P(Di)≤1，(i=l，2，…，L)，∑P(Di)=1。
　　对于两类故障诊断问题，就相当于在识别前已知正常状态D1的概率户(D1)和异常状态0：的概率P(D2)，它们是由先验知识确定的状态先验概率。如果不做进一步的仔细观测，仅依靠先验概率去作决策，那么就应给出下列的决策规则：若P(D1)>P(D2)，则做出状态属于D1类的决策；反之，则做出状态属于D2类的决策。例如，某设备在365天中，有故障是少见的，无故障是经常的，有故障的概率远小于无故障的概率。因此，若无特B，j明显的异常状况，就应判断为无故障。显然，这样做对某一实际的待检状态根本达不到诊断的目的，这是由于只利用先验概率提供的分类信息太少了。为此，我们还要对系统状态进行状态检测，分析所观测到的信息。