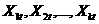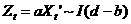协整 发表评论(0) 编辑词条

经典回归模型是建立在平稳数据变量的基础之上的，对于非平稳变量，不能使用经典回归模型，否则会出现虚假回归等诸多问题。由于许多经济问题是非平稳的，这就给经典的回归分析方法带来了很大限制。由于实际应用中大多数时间序列是非平稳的，通常采用差分方法消除序列中含有的非平稳趋势，使得序列平稳化后建立模型，比如使用ARIMA模型。但是变换后的序列限制了所讨论经济问题的范围，并且有时变换后的序列由于不具有直接的经济意义，使得化为平稳序列后所建立的时间序列模型不便于解释。

1987年Engle和Granger提出的协整理论及其方法，为非平稳序列的建模提供了另一种途径。虽然一些经济变量的本身是非平稳序列，但是，它们的线性组合却有可能是平稳序列。这种平稳的线性组合被称为协整方程，且可解释为变量之间的长期稳定的均衡关系。
例如，消费和收入都是非平稳时间序列，但是具有协整关系。假如它们不具有，那么长期消费就可能比收入高或低，于是消费者便会非理性地消费或累积储蓄。
假定一些经济指标被某经济系统联系在一起，那么从长远看来这些变量应该具有均衡关系，这是建立和检验模型的基本出发点。在短期内，因为季节影响或随机干扰，这些变量有可能偏离均值。如果这种偏离是暂时的，那么随着时间推移将会回到均衡状态；如果这种偏离是持久的，就不能说这些变量之间存在均衡关系。协整(co-integration)可被看作这种均衡关系性质的统计表示。
协整概念是一个强有力的概念。因为协整允许我们刻画两个或多个序列之间的平衡或平稳关系。对于每一个序列单独来说可能是非平稳的，这些序列的矩，如均值、方差或协方差随时间而变化，而这些时间序列的线性组合序列却可能有不随时间变化的性质。

k 维向量 Yt = (y1t，y2t，…，ykt) 的分量间被称为d,b阶协整，记为Yt ～ CI (d，b)，如果满足：
(1) y1t，y2t，…，ykt都是 d 阶单整的，即Yt～I (d)，要求 Yt 的每个分量 yit ～I (d)；
(2) 存在非零向量β= (β1, β2 , …, βk )，使得β‘ Yt～I (d-b)，0 <b≤d，

简称 Yt 是协整的，向量β又称为协整向量。

长期均衡关系与协整

经济理论指出，某些经济变量间确实存在着长期均衡关系。这种均衡关系意味着经济系统不存在破坏均衡的内在机制。如果变量在某时期收到干扰后偏离其长期均衡点，则均衡机制将会在下一期进行调整以便使其重新回到均衡状态。

长期均衡关系 

假设X,Y之间的长期均衡关系可以用描述为：

模型揭示了X,Y之间的长期稳定的均衡关系，但其中一个重要的假设是随机干扰项必须是平稳序列。如果随机干扰项具有随机性趋势，会导致Y对其均衡点的任何偏离都会被长期累积下来而不能被消除。而协整模型就是用来表示这种长期的均衡关系的。

一般的，如果对

存在向量a，使得

其中b>0，则认为Xt~CI(d,b),a为协整向量。

注意：
(1) 作为对非平稳变量之间关系的描述，协整向量是不惟一的；
(2) 协整变量必须具有相同的单整阶数；

(3) 最多可能存在 k-1个线性无关的协整向量 ( yt 的维数是 k )；

(4) 协整变量之间具有共同的趋势成分，在数量上成比例 。

这种协整检验方法是对回归方程的残差进行单位根检验。从协整理论的思想来看，自变量和因变量之间存在协整关系。 也就是说，因变量能被自变量的线性组合所解释，两者之间存在稳定的均衡关系，因变量不能被自变量所解释的部分构成一个残差序列，这个残差序列应该是平稳的。
因此，检验一组变量（因变量和解释变量）之间是否存在协整关系等价于检验回归方程的残差序列是否是一个平稳序列。通常地，可以应用ADF检验来判断残差序列的平稳性，进而判断因变量和解释变量之间的协整关系是否存在。
协整检验的目的是决定一组非稳定序列的线性组合是否具有协整关系，也可以通过协整检验来判断线性回归方程设定是否合理、稳定，这两者的检验思想和过程是完全相同的。
利用ADF的协整检验方法来判断残差序列是否平稳，如果残差序列是平稳的，则回归方程的设定是合理的，说明回归方程的因变量和解释变量之间存在稳定的均衡关系。反之，说明回归方程的因变量和解释变量之间不存在稳定均衡的关系，即便参数估计的结果很理想，这样的一个回归也是没有意义的，模型本身的设定出现了问题，这样的回归是一个伪回归。

Engle和Granger于1987年提出两步检验法。

第一步，用OLS方法估计长期均衡关系，得到回归系数，这一步通常称为协整回归或静态回归。

第二步，检验残差的单整性；如果残差为平稳序列，则认为协整关系存在；否则认为协整关系不存在。