补集 发表评论(0) 编辑词条

　　定义:
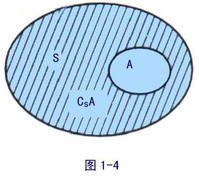
　　一般地,设S是一个集合,A是S的一个子集,由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集)记作CuA.
　　在集合论和数学的其他分支中，存在补集的两种定义：相对补集和绝对补集。
　　补集可以看作两个集合相减，有时也称作差集。
　　1：若 A，B，C 是集合，则下列恒等式成立：
　　C − (A ∩B) = (C − A) ∪(C − B)
　　C − (A ∪B) = (C − A) ∩(C − B)
　　C − (B − A) = (A ∩C) ∪(C − B)
　　(B − A) ∩C = (B ∩C) − A = B ∩(C − A)
　　(B − A) ∪C = (B ∪C) − (A − C)
　　A − A = Φ
　　Φ; − A =Φ ;
　　A − Φ = A
　　若给定全集 U，则 A 在 U 中的相对补集称为 A 的绝对补集（或简称补集），写作 CA，即：
　　CA = U − A
　　与补集有关的运算规律
　　求补律
　　A∪CuA=S
　　A∩CuA=Φ