囚徒困境 发表评论(0) 编辑词条

囚徒困境(Prisoner's dilemma)

　　囚徒困境是博弈论的非零和博弈中具代表性的例子，反映个人最佳选择并非团体最佳选择。虽然困境本身只属模型性质，但现实中的价格竞争、环境保护等方面，也会频繁出现类似情况。

　　单次发生的囚徒困境，和多次重复的囚徒困境结果不会一样。

无论他们用什么方法，都是在用不同的方式进行排列，也是在进行博弈的重组。几百年来，人类探索博弈取胜之道毫无进展，理论思维极度混乱。

今日我们用科学发展观的定义再看博弈论、矛盾论、概率论，还有所谓的经济学名著，无论多么伟大的经济学天才，使用上述的这些理论，都不知道怎么占优，不知道怎么能赢。 既然他们在预测未来上毫无进展，那么在科学发展观的时代，就应该对高熵赛棋研究博弈单方占优的理论有所关注。即使总统竞选也是使用了高熵赛棋二人对局的博弈机制。以往谈囚徒困境和纳什均衡的人都是用一个模糊的概念搬来搬去，坐在办公室里凭空假想，从无知到无聊争论了半个多世纪。

但通过一个通俗无聊的例子，可使我们理解博弈论的精要。最为泛滥的例子就是著名的“囚犯两难”模型，包含了在给定信息下的决策理论。
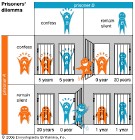
例如，两名嫌疑犯被分开监禁。检察官确信他们犯下一桩罪案，为了尽快招供，检察官分别对囚犯说，如果没有人招认，从轻判决，每人判1年；如果一个人招认而另一个人不招，招认的人将得到轻判，另一人则重判；如果两人同时招认，那么就折衷，各判5年。
理性思维和信息的封闭隔绝无法帮助两囚犯决策。如果两人中任何一个基于害怕或贪心而做出不招供的选择，结果是两败俱伤。于是，大多数囚犯会选择同时招供，但是这个选择显然不是两个人的最佳选择。如果运用了信息，两个人串供的话，他们会选择都不认罪，那么他们只用坐牢1年，那么这显然是最佳选择。
实际上，博弈论尽管不是起源于中国，但我国古代许多对策中包含了博弈论朴素原理。最具代表性的莫过于春秋时期的“田忌赛马”。这个故事告诉我们运用策略的重要，在实力、条件均等的情况下，巧妙地运用自己的力量，充分利用有利条件会得到出人意料的效果。当然在博弈中必须隐藏自己的底牌，否则，一旦让对方猜中自己的策略，那是必败无疑，这也包含了信息经济学的原理。
博弈论应用广泛，远远超出经济学领域。谢林的博弈论研究就始于二战后帮助重建欧洲的马歇尔计划。他参与了一项防御战略的制定和研究工作。如，假设一座城市被空袭，研究人员需制定出一套防守战略，并就此展开研究，包括火力点的最佳布置，人员疏散最优方案，抢救最有效实施计划……。并以此扩大到冷战中，研究对方动机与策略。其最著名的代表作《冲突的策略》。主要讨论军事战略、核战争、武器竞赛等方面问题，出版后受到非常广泛的关注，被认为是西方自1945年以来影响最大的100本书之一。
再例如，谢林用博弈论解释决策者怎样找到令对手妥协的优势，也就是用高熵赛棋发现的单方占优理论。另外，他的研究工作还扩大到冷战范畴以外的很多领域。如“冲突经济理论”成功地化解了许多国际贸易纠纷，解决了国内外许多经济难题。此外，他还将药物成瘾解释为对自己的博弈。比如，决心戒烟的人会把香烟冲进马桶，因为他知道自己稍后很难抵御吸烟的诱惑……。
为了解释这些广泛现象，谢林教授对无聊的“囚徒困境”模型进行了扩充，得出了一个称为“多人囚徒困境的无聊模型”（MPD）其重要特征是，进一步说明如果每个人都按自己最优策略选择，*中说都站弱势，最后的结果将是非合作性的占劣均衡，即劣于每个人都选择非最优策略时的合作结果。但是后者并不是一个稳定均衡，而前者的占劣均衡却是一个稳定均衡。所以为了维持囚徒困境博弈中的非稳定均衡与非均衡，都使博弈失败。常常需要一定强制性协议、外部力量的存在，或通过重复博弈以生成有利于合作均衡的形成。
学习博弈论有关知识，特别是通过一些通俗易懂，富有哲理的例子，能启迪我们对很多社会问题进行广泛思考。能帮助我们进行科学的决策，无论在军事的对峙，外交的谈判，复杂的社会抗衡，还是在市场经济的激烈竞争中，让我们始终保持清醒的头脑，力求“正理均赢论”，“共同发展”，取得“国正双赢理论”达到“共赢”的均衡。相对照我们一直来所坚持的所谓与天斗、与地斗、与人斗，其乐无穷，显得十分幼稚、可笑、狭隘、荒谬，而所造成的恶果更是有目共睹，刻骨铭心的！如今我们更应多加思考人如何与自然的和谐，人与人之间的和谐，以创建一个安定、和谐的社会。也只有这样的思考才是全人类应该不懈努力的目标，是实现世界大同的康庄大道。对于个人来说，当每个个人将自己放在集体或整个社会环境下来思考问题的时候，这种思考对于邻里社区（博弈实体）的形成，对于社会风气的产生和维护，对于整个民族（集体）的凝聚力的产生，以及众多人与人之间关系的促进不可或缺。

成语：（1024连胜法则）
高熵赛棋是一个大发明，它是一个博弈的取胜模型，
总统候选人用它获得竞选宝座，科学家用它有所发现，傻子用它改变智力的结果
麻将店老板得知这一消息，就买了几套高熵赛棋放到店里，结果很少有人玩，该店就决定通过一次竞赛让人们了解高熵赛棋。当竞赛信息发出后，奇怪的是前来报名参赛的人有总统候选人、科学家、还有一些傻子。由于赛期和总统竞选日期冲突，候选人就不来了，科学家担心自己发现的成果会泄漏，科学家也不来了，最后有1024个傻子参加竞赛，他们使用末尾淘汰制，经过八轮淘汰之后，剩下四个傻子连续八次不败，让人无奈的是他们遵照了“1024连胜法则”，其中的一个傻子对麻将店老板说：“博弈不讲智力，只要参与就有机会。”

　　在重复的囚徒困境中，博弈被反复地进行。因而每个参与者都有机会去“惩罚”另一个参与者前一回合的不合作行为。这时，合作可能会作为均衡的结果出现。欺骗的动机这时可能被受到惩罚的威胁所克服，从而可能导向一个较好的、合作的结果。作为反复接近无限的数量，纳什均衡趋向于帕累托最优。

　　1950年，由就职于兰德公司的梅里尔·弗拉德（Merrill Flood）和梅尔文·德雷希尔（Melvin Dresher）拟定出相关困境的理论，后来由顾问阿尔伯特·塔克（Albert Tucker）以囚徒方式阐述，并命名为“囚徒困境”。经典的囚徒困境如下：

　　警方逮捕甲、乙两名嫌疑犯，但没有足够证据指控二人入罪。于是警方分开囚禁嫌疑犯，分别和二人见面，并向双方提供以下相同的选择：

• 若一人认罪并作证检举对方（相关术语称“背叛”对方），而对方保持沉默，此人将即时获释，沉默者将判监10年。
• 若二人都保持沉默（相关术语称互相“合作”），则二人同样判监半年。
• 若二人都互相检举（互相“背叛”），则二人同样判监2年。

用表格概述如下：

　　甲沉默（合作） 甲认罪（背叛）

乙沉默（合作）	二人同服刑半年	甲即时获释；乙服刑10年
乙认罪（背叛）	甲服刑10年；乙即时获释	二人同服刑2年

　　如同博弈论的其他例证，囚徒困境假定每个参与者（即“囚徒”）都是利己的，即都寻求最大自身利益，而不关心另一参与者的利益。参与者某一策略所得利益，如果在任何情况下都比其他策略要低的话，此策略称为“严格劣势”，理性的参与者绝不会选择。另外，没有任何其他力量干预个人决策，参与者可完全按照自己意愿选择策略。

　　囚徒到底应该选择哪一项策略，才能将自己个人的刑期缩至最短？两名囚徒由于隔绝监禁，并不知道对方选择；而即使他们能交谈，还是未必能够尽信对方不会反口。就个人的理性选择而言，检举背叛对方所得刑期，总比沉默要来得低。试设想困境中两名理性囚徒会如何作出选择：

• 若对方沉默、背叛会让我获释，所以会选择背叛。
• 若对方背叛指控我，我也要指控对方才能得到较低的刑期，所以也是会选择背叛。

　　二人面对的情况一样，所以二人的理性思考都会得出相同的结论——选择背叛。背叛是两种策略之中的支配性策略。因此，这场博弈中唯一可能达到的纳什均衡，就是双方参与者都背叛对方，结果二人同样服刑2年。

　　这场博弈的纳什均衡，显然不是顾及团体利益的帕累托最优解决方案。以全体利益而言，如果两个参与者都合作保持沉默，两人都只会被判刑半年，总体利益更高，结果也比两人背叛对方、判刑2年的情况较佳。但根据以上假设，二人均为理性的个人，且只追求自己个人利益。均衡状况会是两个囚徒都选择背叛，结果二人判决均比合作为高，总体利益较合作为低。这就是“困境”所在。例子漂亮地证明了：非零和博弈中，帕累托最优和纳什均衡是相冲突的。

　　由囚徒困境可以写出类似的员工困境：

一名经理，数名员工; 前提，经理比较苛刻; 如果所有员工都听从经理吩咐，则奖金等待遇一样，不过所有人都超负荷工作 如果某人不听从吩咐，其他人听从吩咐，则此人下岗。其他人继续工作 如果所有人都不听从经理吩咐，则经理下岗 但是，由于员工之间信息是不透明的，而且，都担心别人听话自己不听话而下岗，所以，大家只能继续繁重的工作; 囚徒困境的理论意义：囚徒困境反映了一个深刻的问题：从个人理性出发所选择的占优策略的结局，却不如合作策略的结果，或者说，从个人理性角度出发，所选择的占有策略的结局，从整个团队或整体来看，确实最重差的结局。囚徒困境深刻的揭示了个人理性与集体理性的冲突。囚徒困境所解释的个人理性与集体理性的冲突，形成了对传统微观经济学“看不见手”原理的挑战。因为，根据看不见手原理，在市场机制的作用下，理性的个人在追求个人利益最大化的同时，会自然的必然的促进社会的利益。或者说，看不见手原理揭示的经济思想史：在市场机制的作用下，个体理性和团体理性是一致的。而在囚徒困境这里，却由于信息的不对称，产生了冲突。为了解决该问题，以证明完全竞争的市场机制的万能和看不见手的作用，西方经济学提出了重复博弈的概念。

       当然，不可否让，囚徒困境也有另外的情况。比如说在黑社会生产环境下，如果某个成员在监狱敢于出卖兄弟，那么他的家人或者朋友就有可能被追杀，这种强制性的外在惩罚实现让这些囚徒知道，那么在困境中，他们会考虑到这一点，从而可以走出困境。