分层最佳抽样 发表评论(0) 编辑词条

　　分层最佳抽样又称“非比例抽样”，是根据各层基本单位标准差的大小，来确定各层样本数目的抽样方法。

　　在各层基本单位之间的差异过分悬殊、某些层的重要性大于其他层的情况下，采取非比例抽样时，在这些层抽取的样本数就多；反之，抽取的样本数就少。如果采取同时兼顾层的大小和层内差异程度的大小来抽样，则有利于提高综合样本对总体全貌的代表性，并可以提高样本的可信程度。

　　采用分层最佳抽样法，确定各样本数目的计算公式如下：

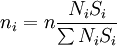
　　式中：

n_i：第i层应抽出的样本数目； n：样本总数目； N_i：第i层的调查单位数； S_i：第i层调查单位的样本标准差。

　　某地有居民20000户，其中高、中、低收入户分别为4000户、12000户、4000户。又已知高收入户的标准差为300元，中收入户的标准差为200元， 低收入户的标准差为100元。现要抽选200户做样本，进行购买力的调查，用分层最佳抽样法分配各层的样本数目。

　　本题中，已知各层居民收入标准差，即：高收入层（n₁）=300、中收入层（n₂）=200、低收入层（n₃）=100。为了便于计算，见列表：

各层次（不同经济收入）	各层的调查单位数（户）Ni	各层的样本标准差（元）Si	乘积NiSi
高 中 低	4000 12000 4000	300 200 100	1200000 2400000 400000
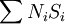	20000		4000000

　　按公式计算，各层的样本数目为：

　　高收入层样本数目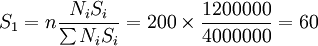：（户）

　　中收入层样本数目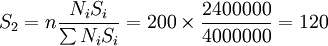：（户）

　　低收入层样本数目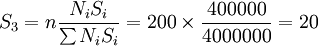：（户）

　　应用分层最佳抽样方法计算出的各层样本抽取数同分层比例抽样法抽出的样本数相比较，可以看出，因各层标准差大小不同，家庭收入高的分层样本增加了20个（从40个变为60个），家庭收入中等的分层样本数，仍然为120个，而家庭收入低的分层样本数减少了20个（从40个变为20个）。高收入户和低收入户在调查总体中单位数都是4000户，为什么从高收入户中产生样本数目是60户，从低收入户中产生样本数目只有20户。这是因为，高收入户的标准差大（300元），从中抽取样本数目就要多一些。低收入户的标准差小（100元），从中抽取的样本数可以少一些。这样抽选到的综合样本比原先仅考虑分层比例抽样得的综合样本更具有对调查总体的代表性，其抽样调查推断的总体结果准确性程度会有所提。

　　从理论上说，各层中的标准差估计值，反映的是各层的单位特征值和各层平均值之间的差异。如果某层中各单位特征值比较接近，差异较小，那么从理论上说，标准差就小。因此，少抽取一些数目的样本，仍然可以代表、反映该层的大致情况。如果某层内各单位差异较大，那么标准差就较大，因而要适当多选一些样本才更合理。